某小天线性能测试

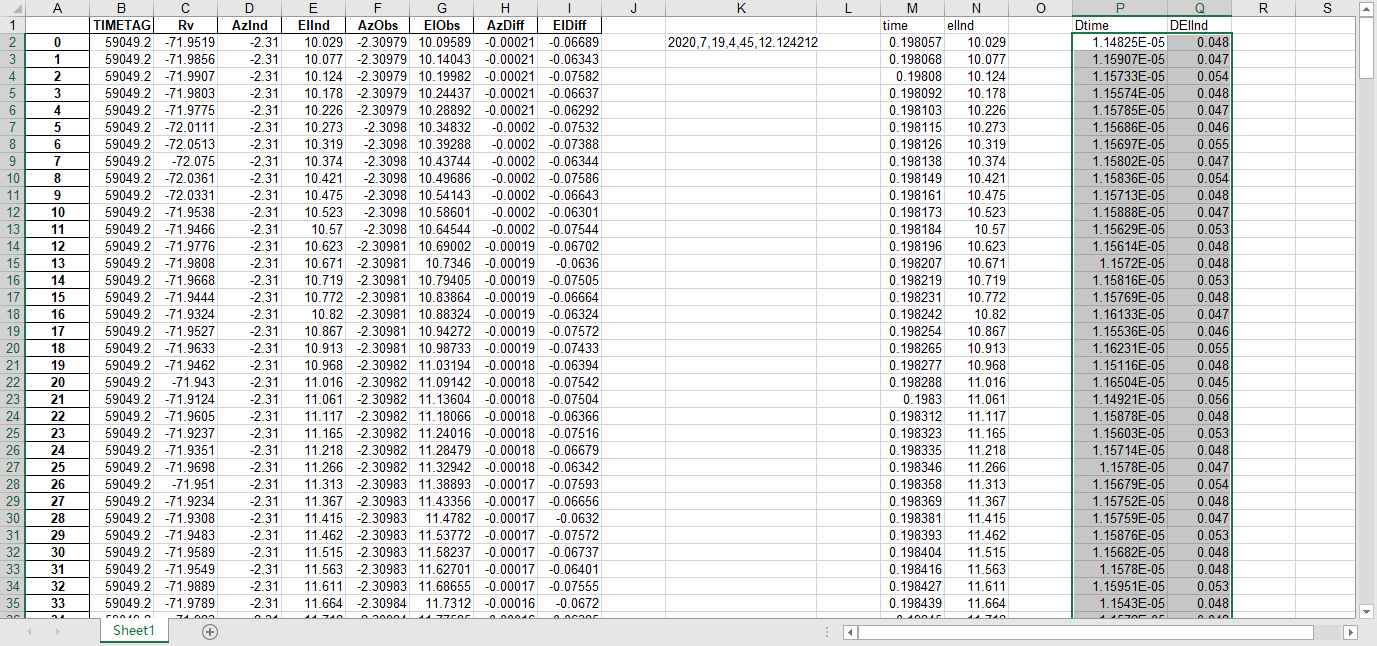
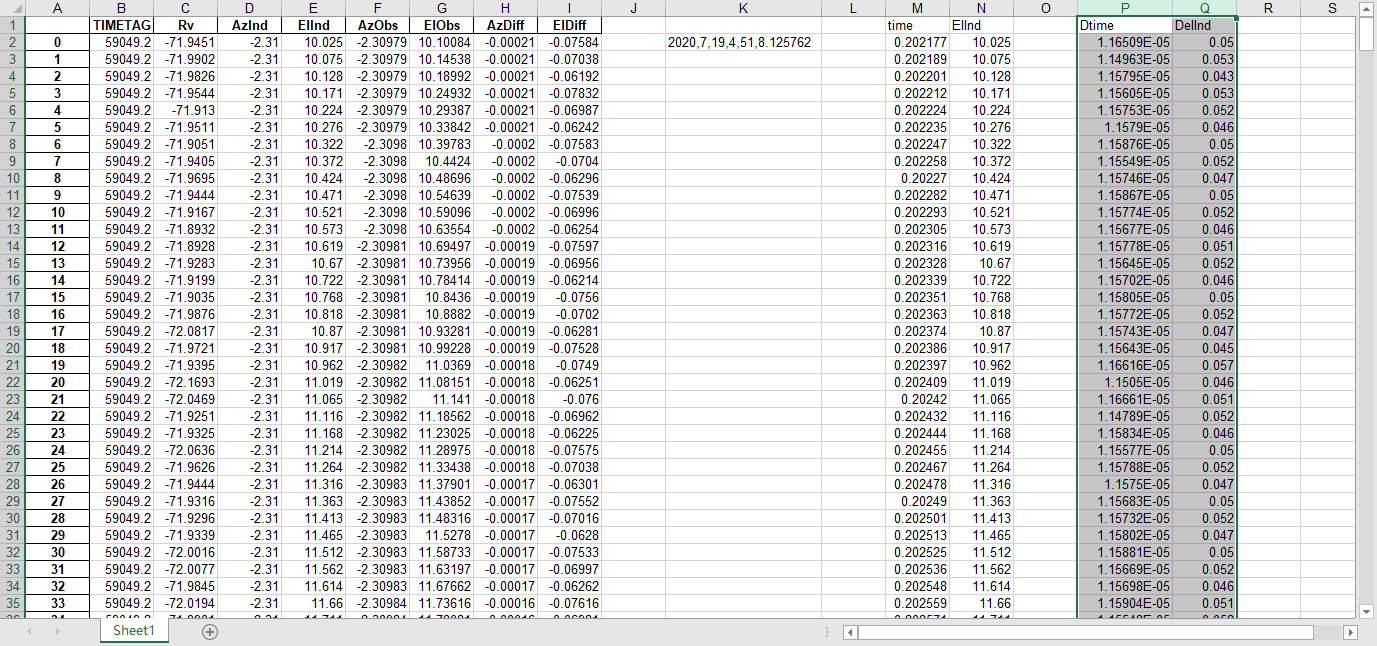
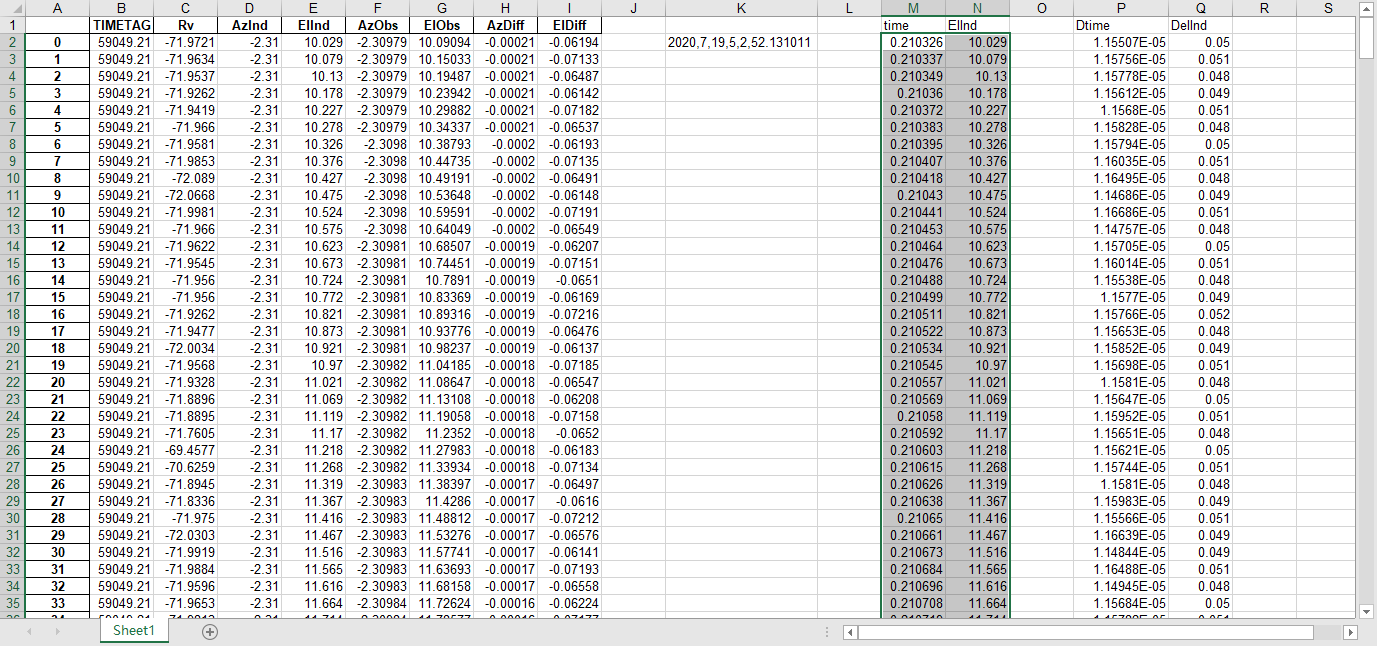
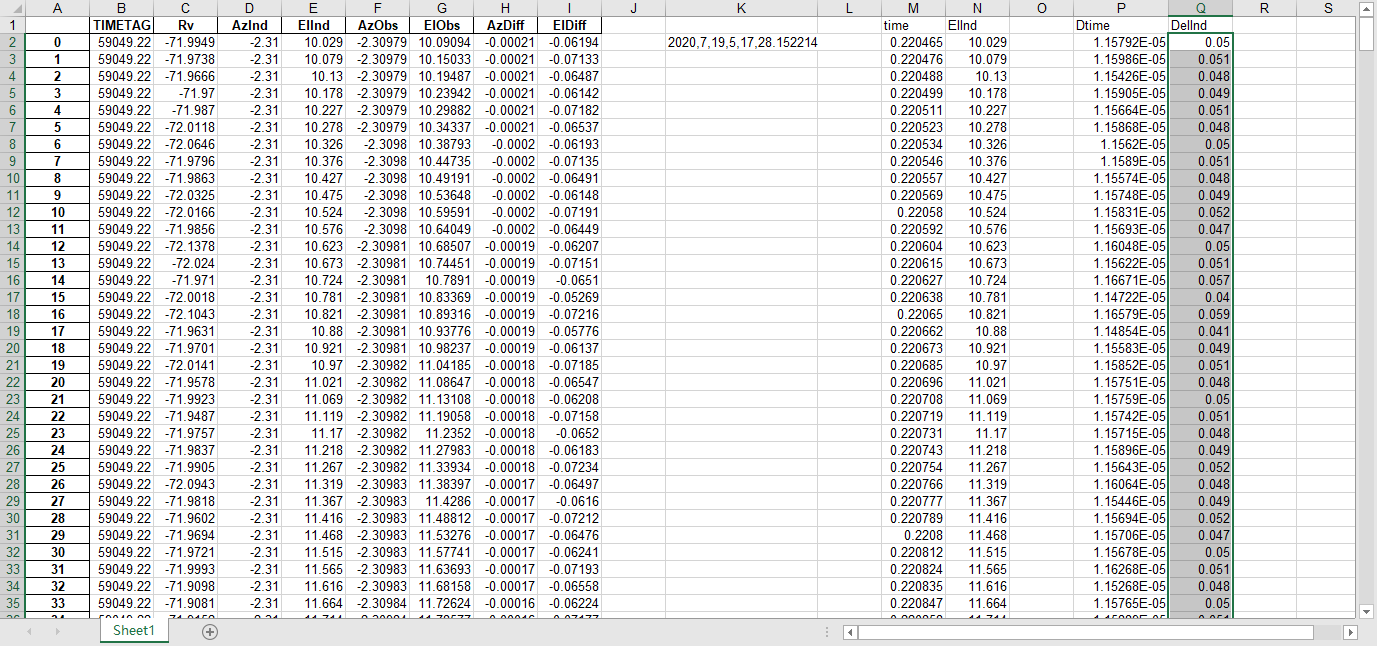
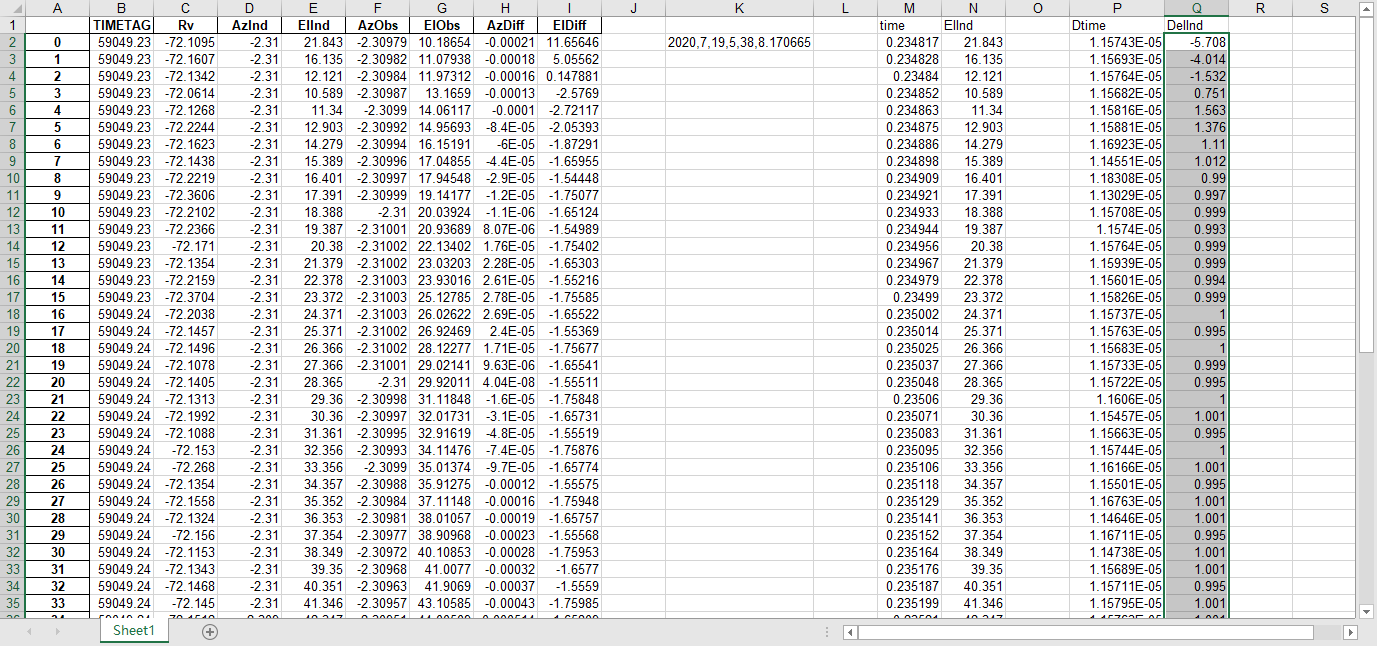
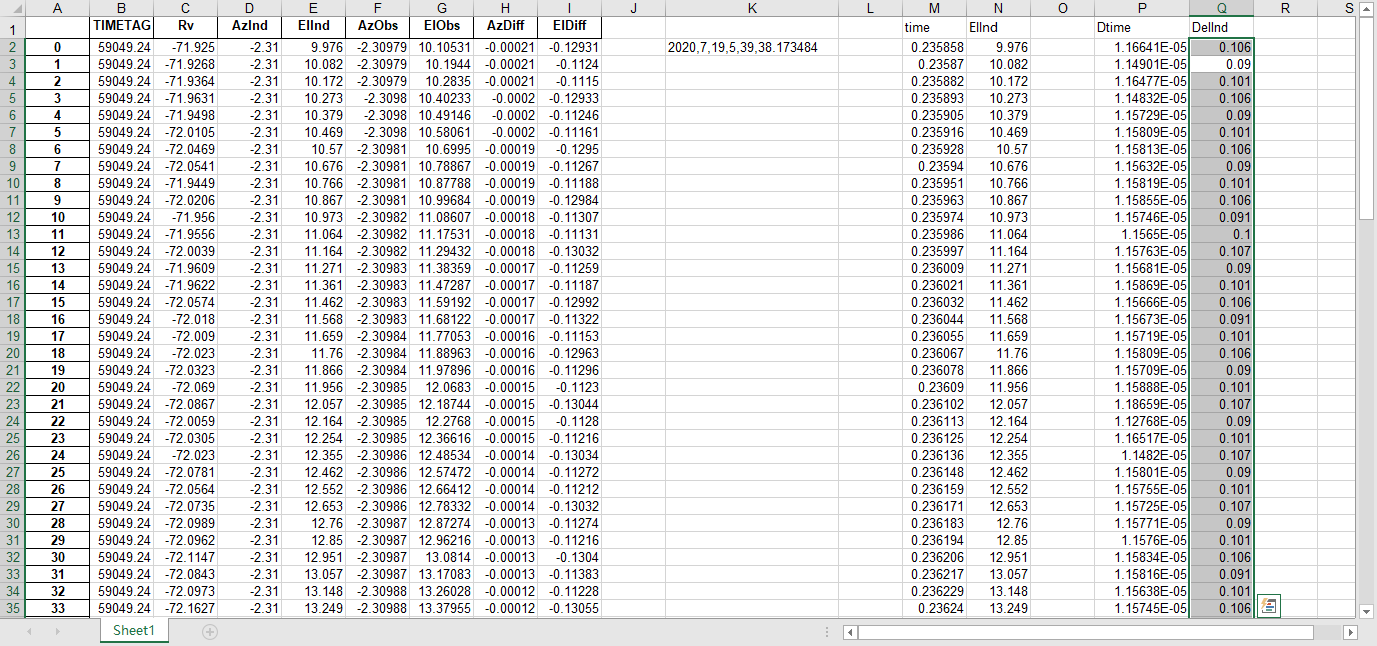
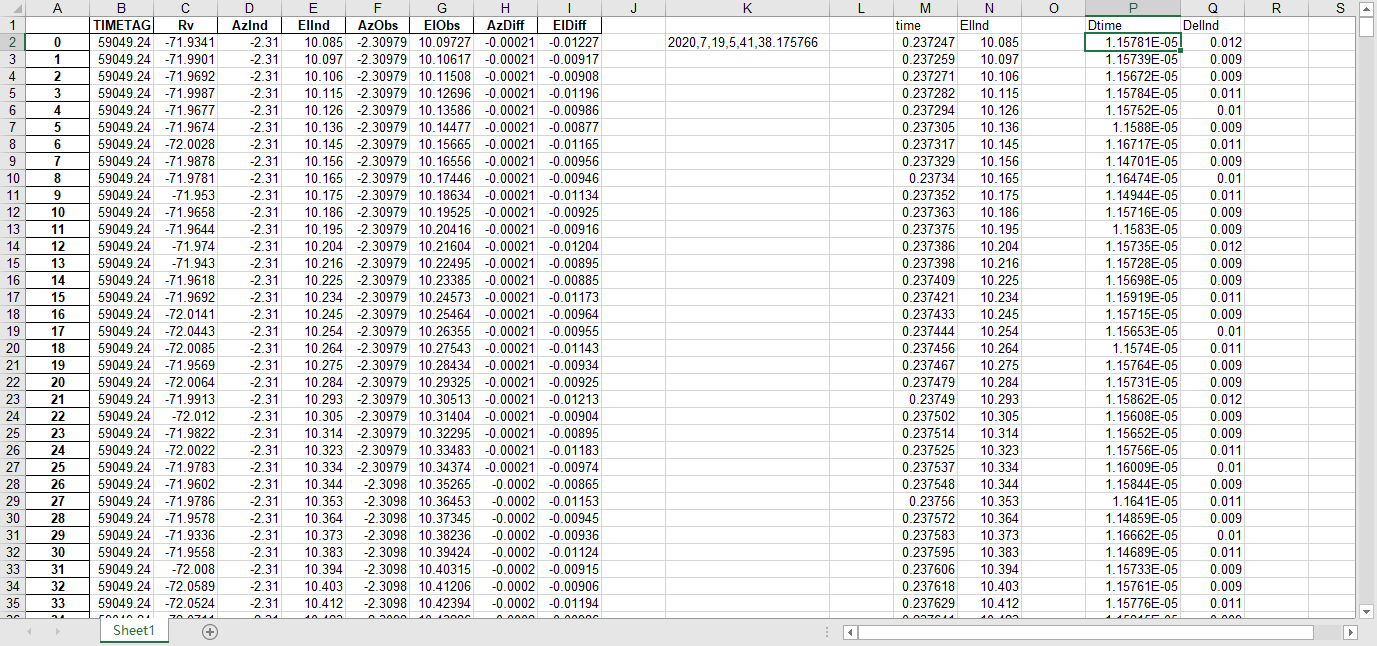
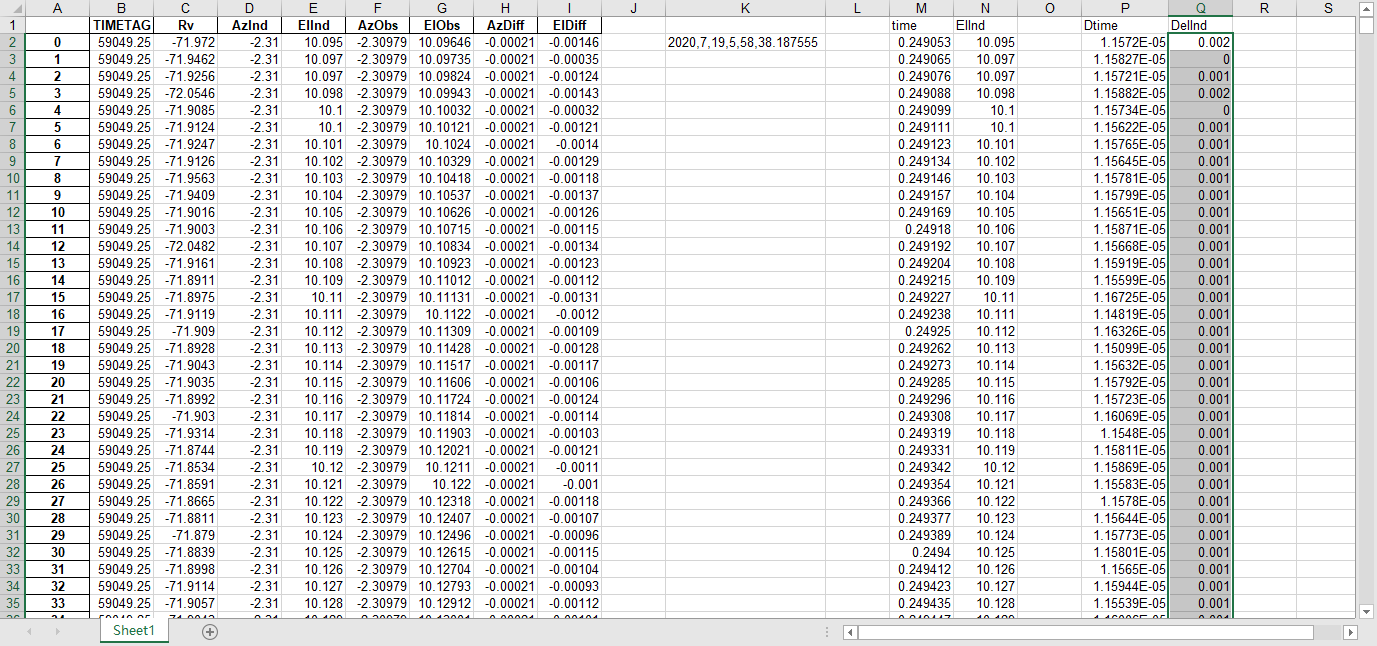
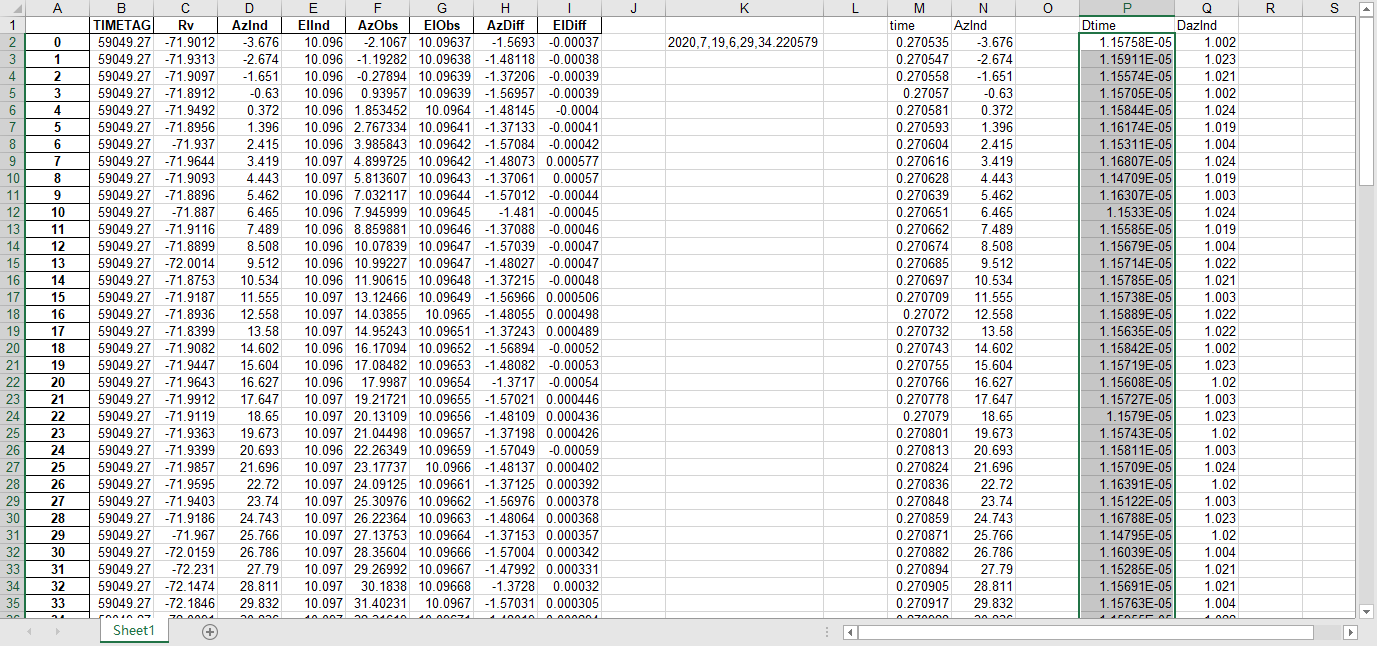
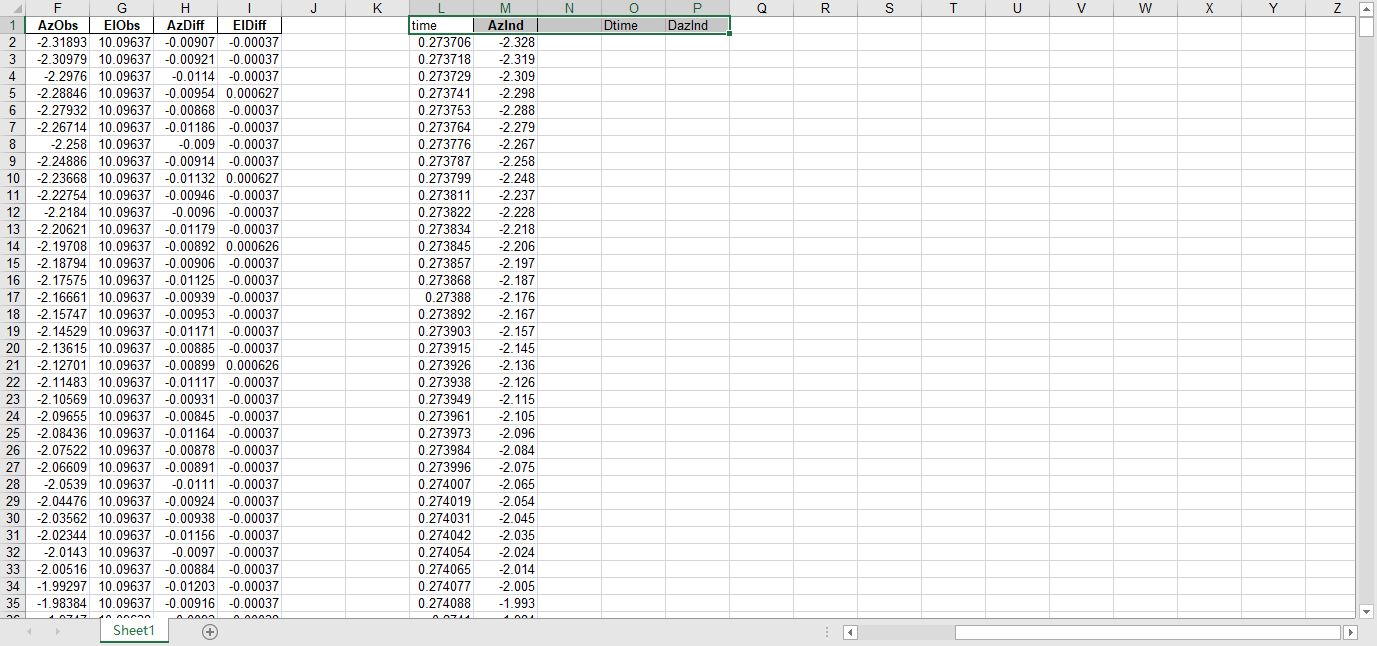
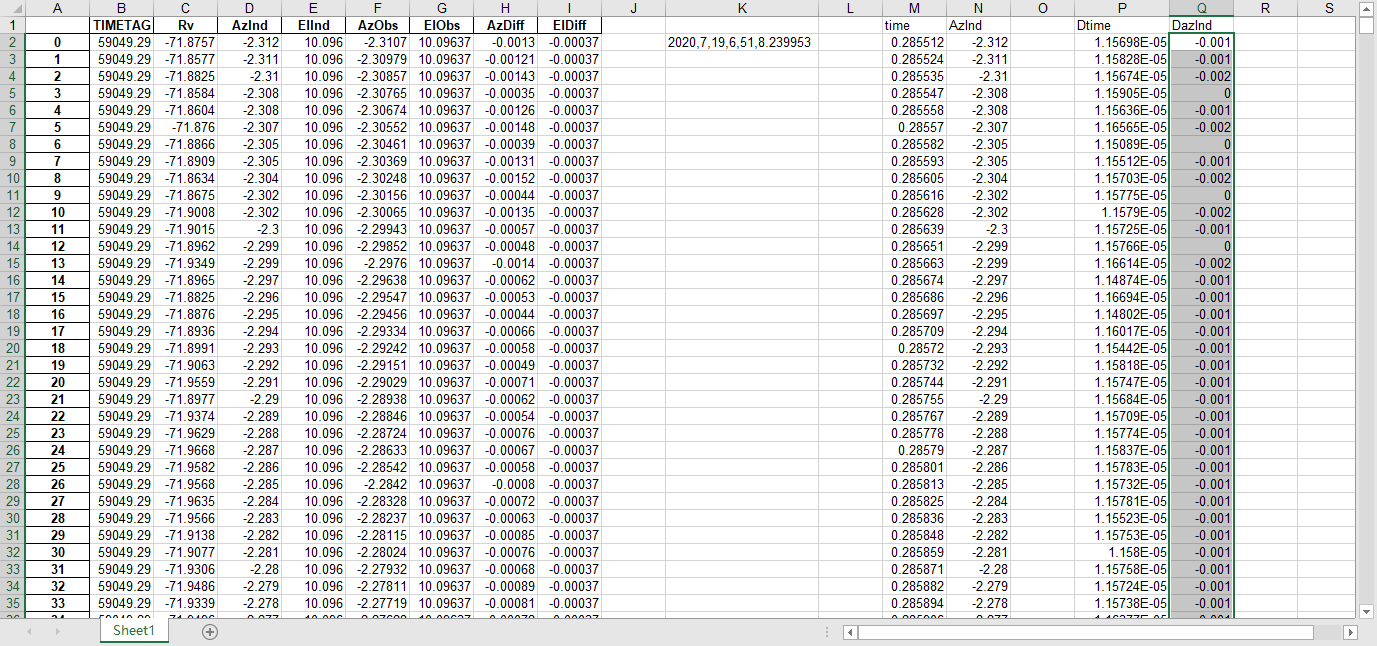
fits文件的头文件提取到excel

import matplotlib.pyplot  as pl

# import pyfits
# from astropy.utils.data import get_pkg_data_filename
from astropy.table import Table
from astropy.io import fits
import pandas as  pd

hdul=fits.open('C:/Users/47459/Downloads/Dcr/2020_07_19_04_32_34.fits')
events=Table.read(hdul,hdu=1)
df=events.to_pandas()
df.to_excel('C:/Users/47459/Downloads/Dcr/2020_07_19_04_32_34.excel')
pd.read_excel('C:/Users/47459/Downloads/Dcr/2020_07_19_04_32_34.xls',sheet_name="Sheet1",index_col=1)

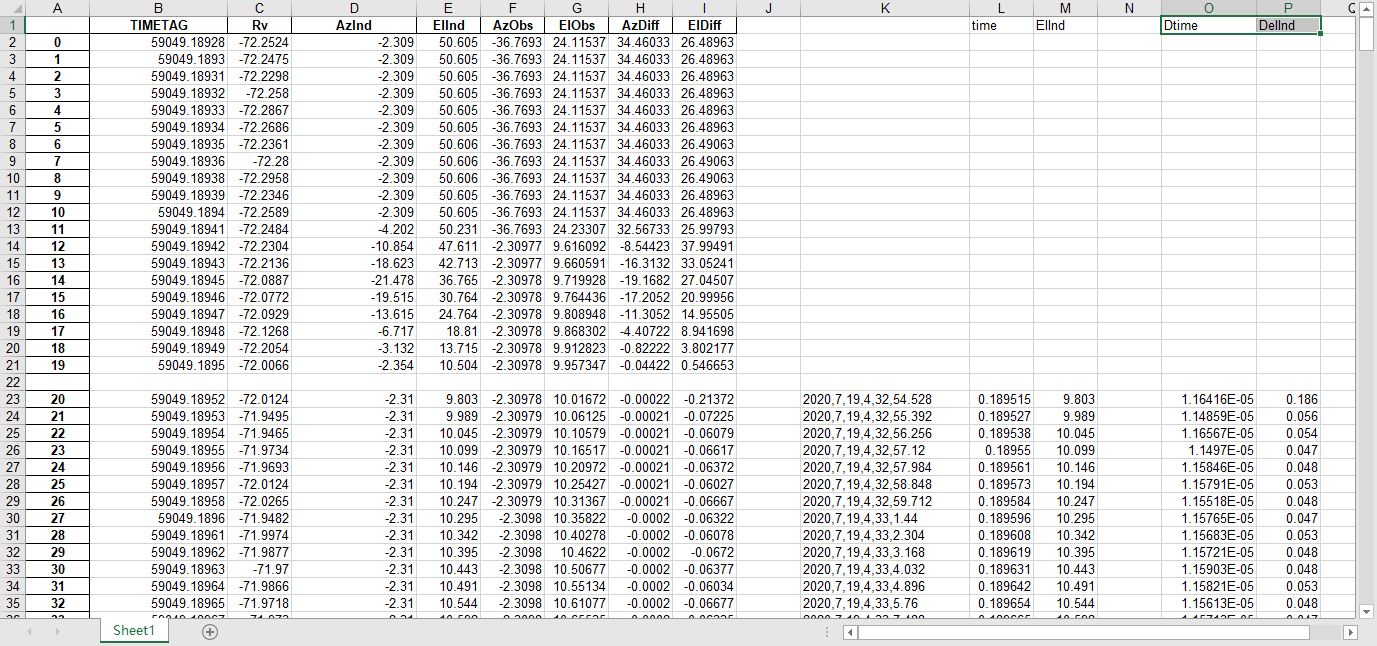
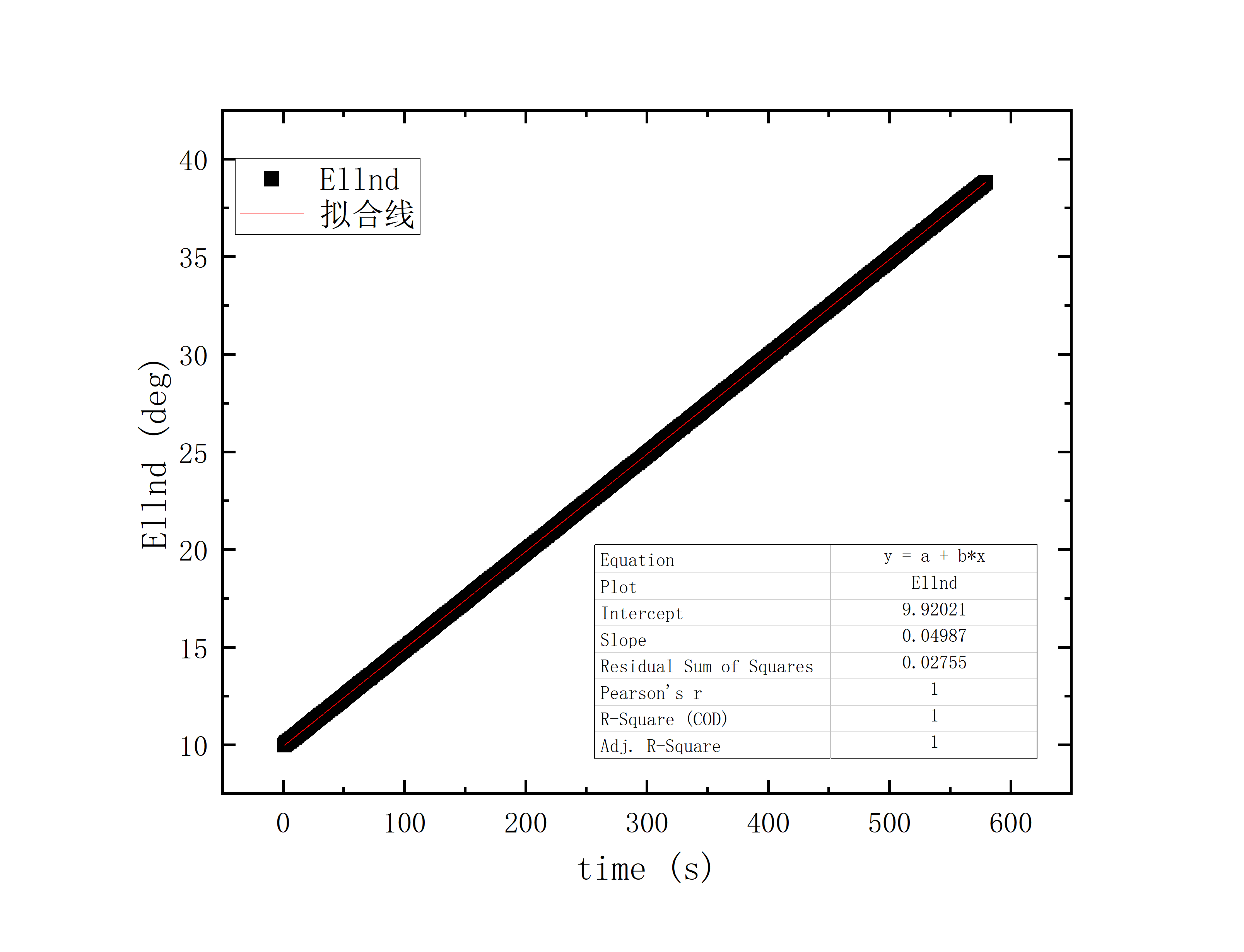
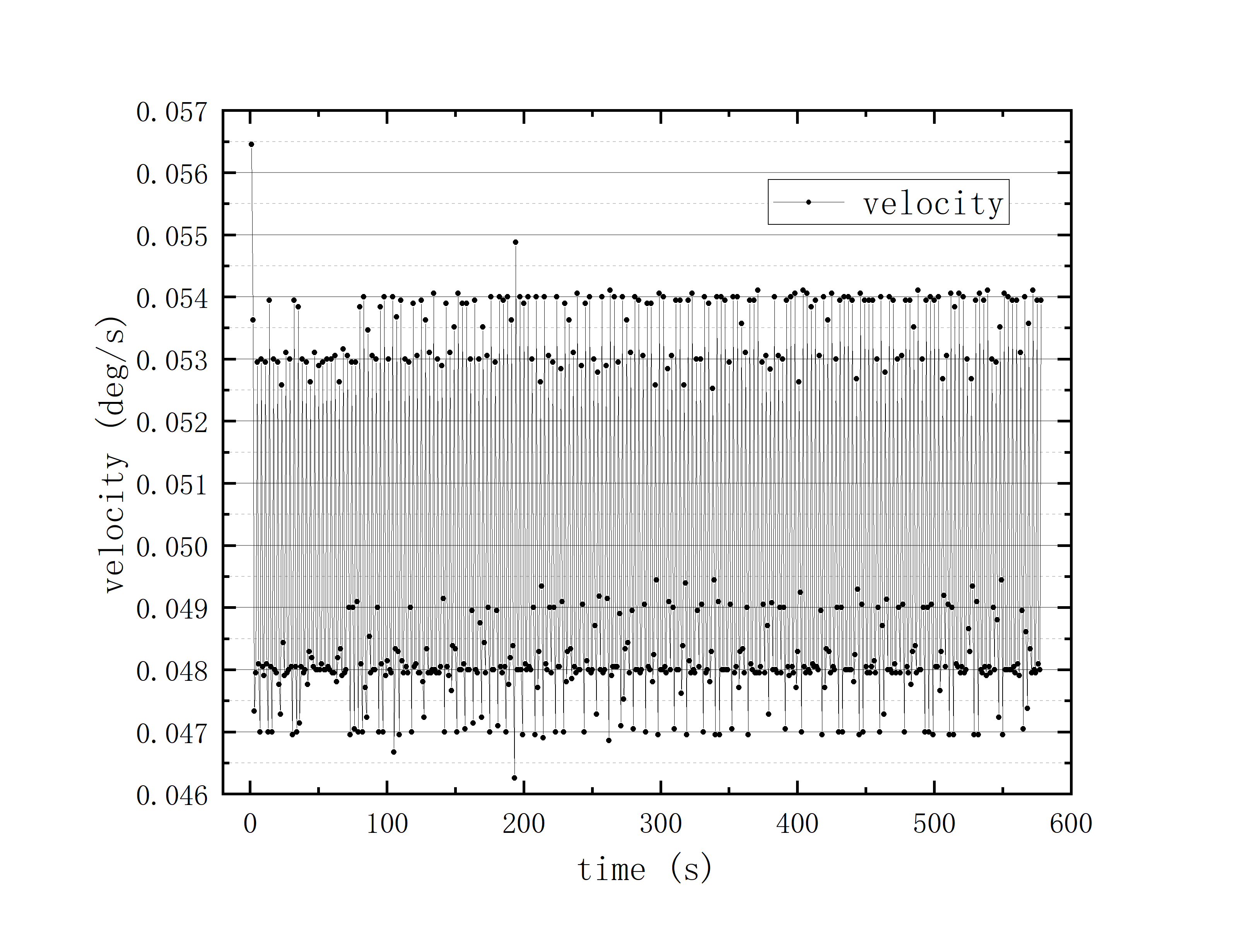
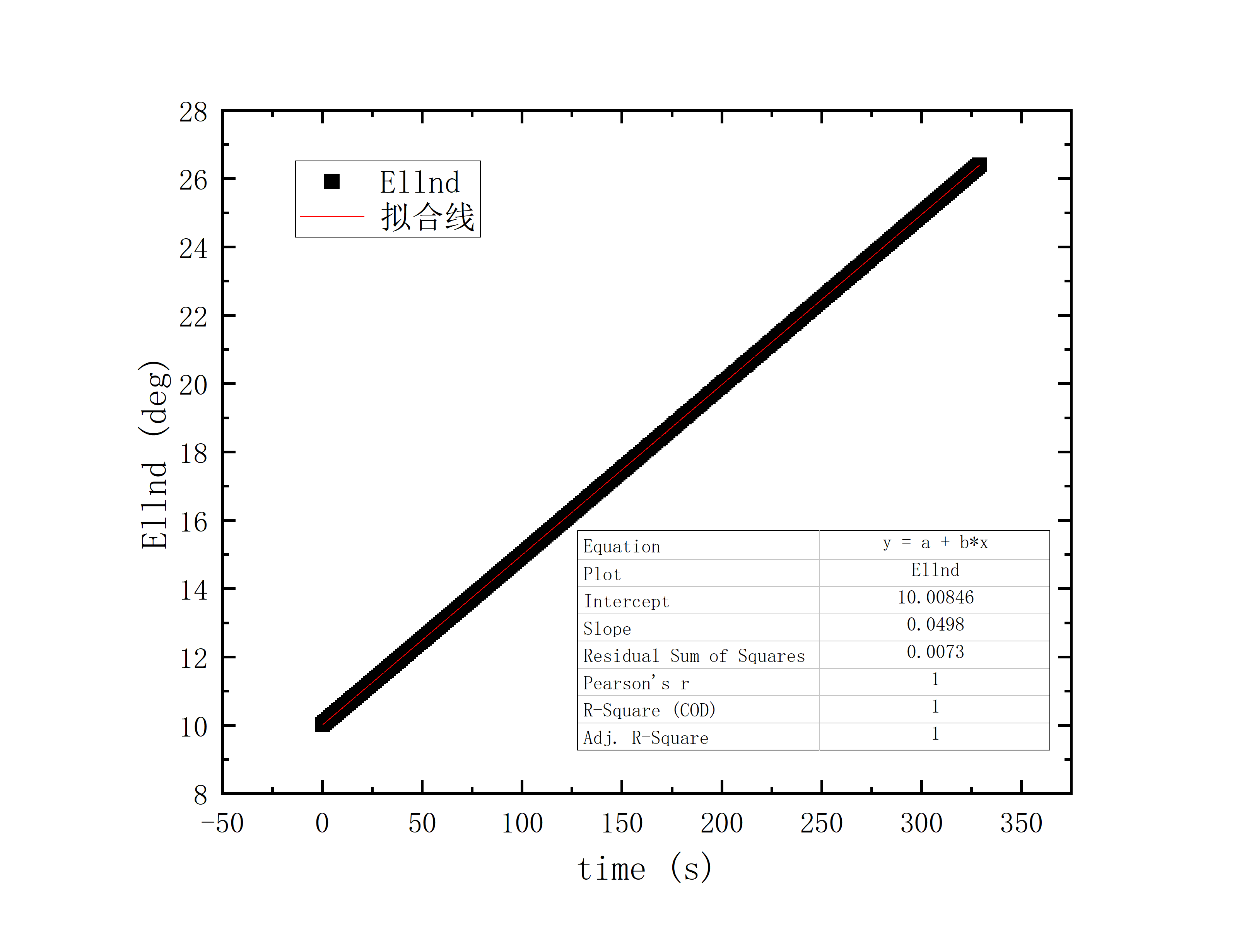
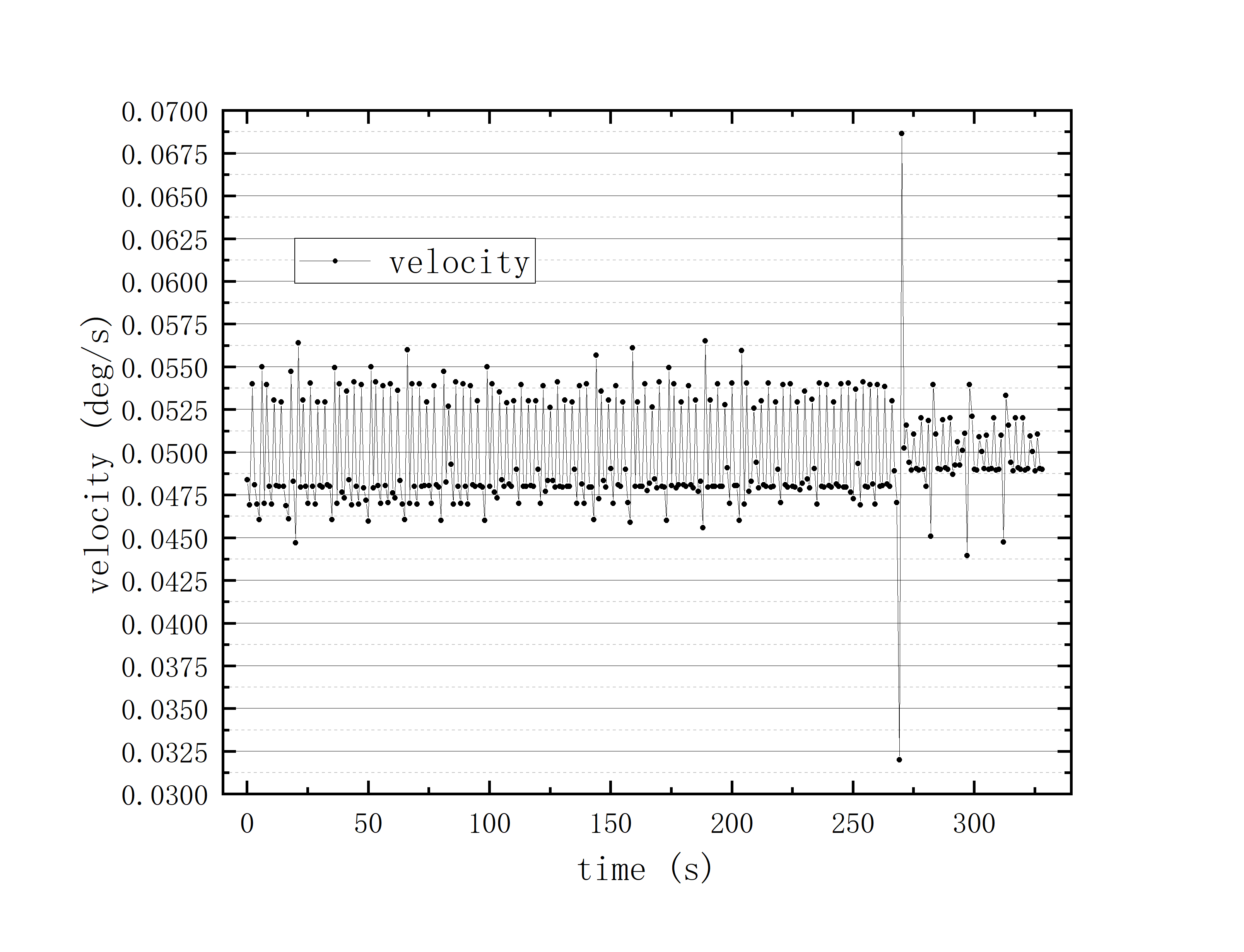
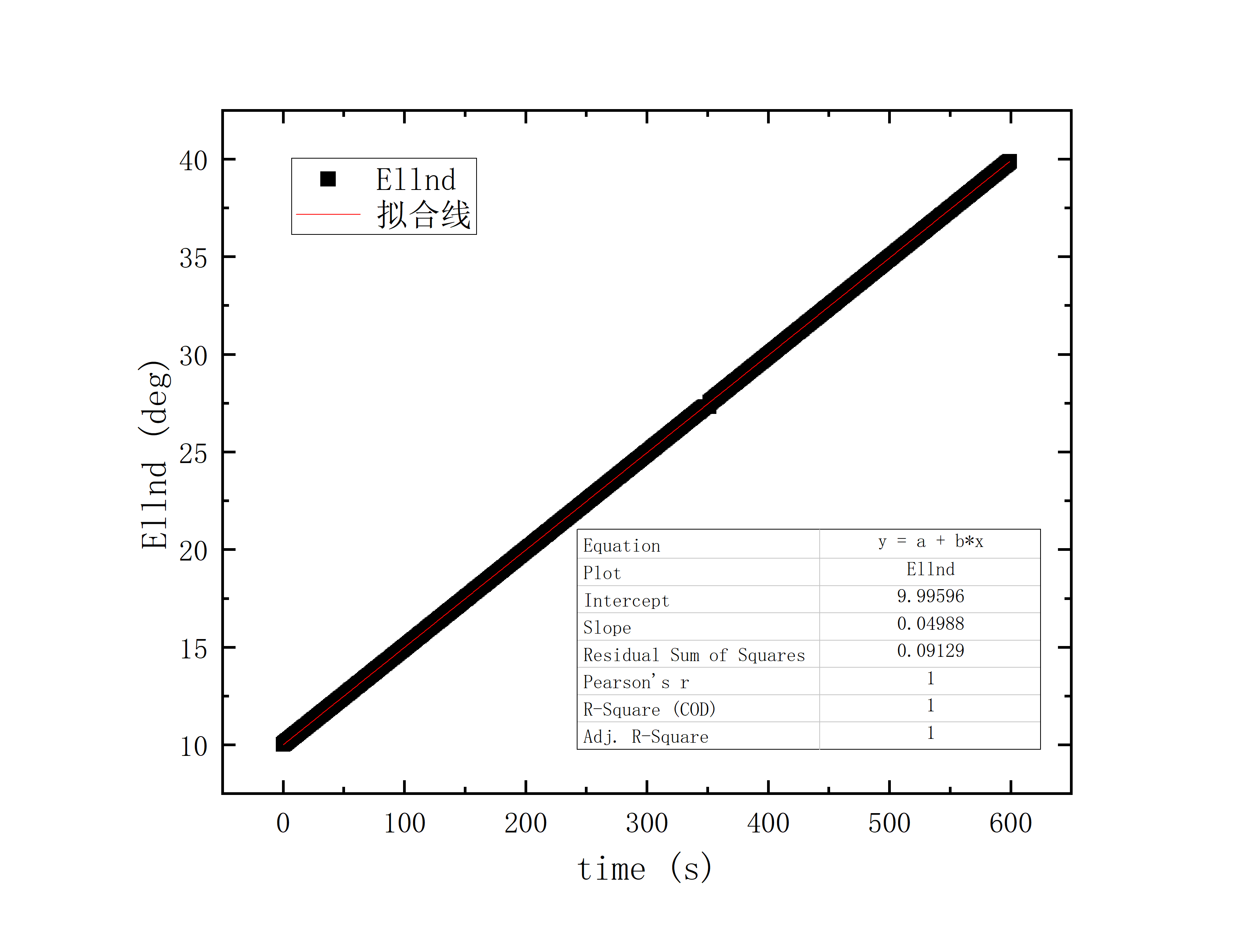
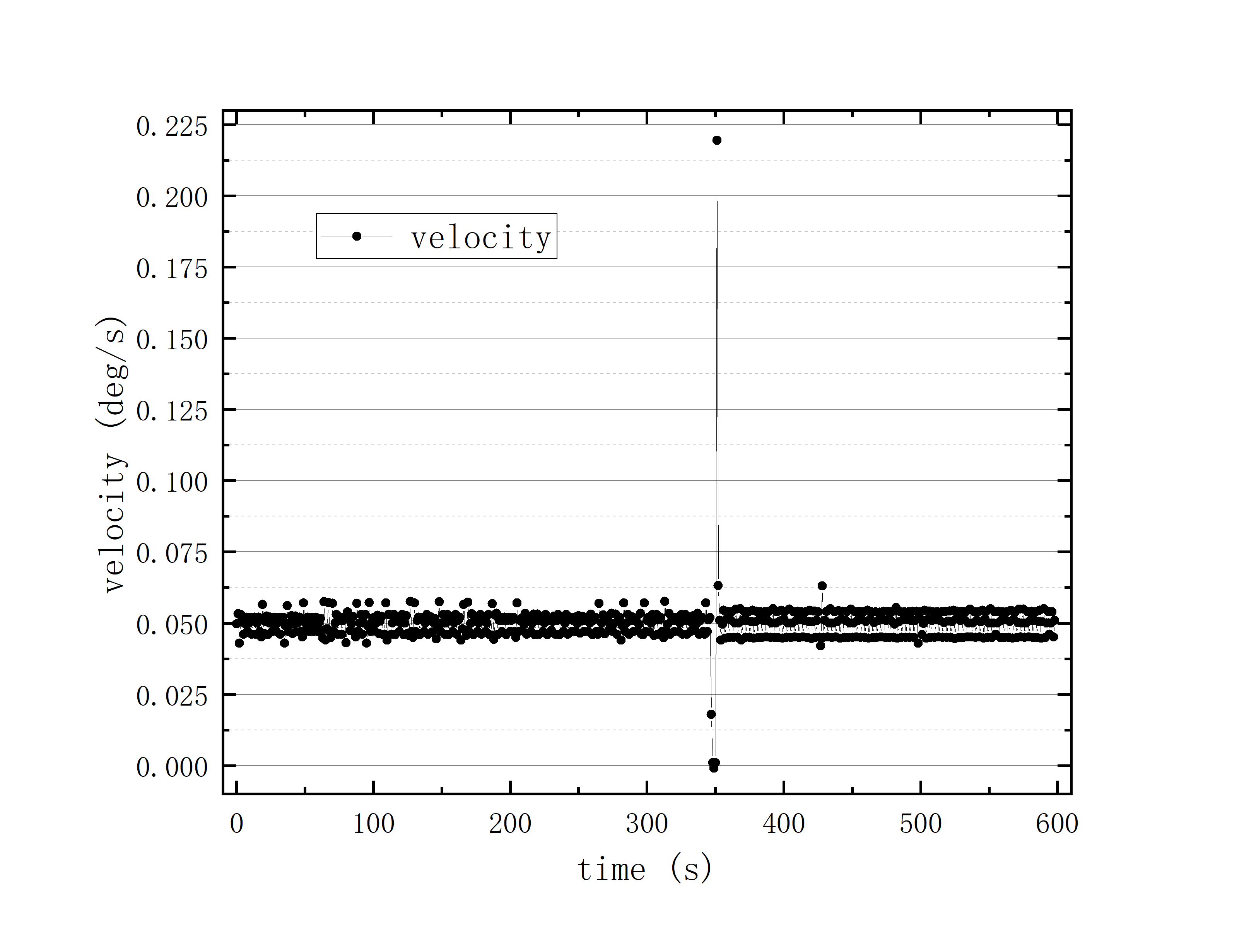
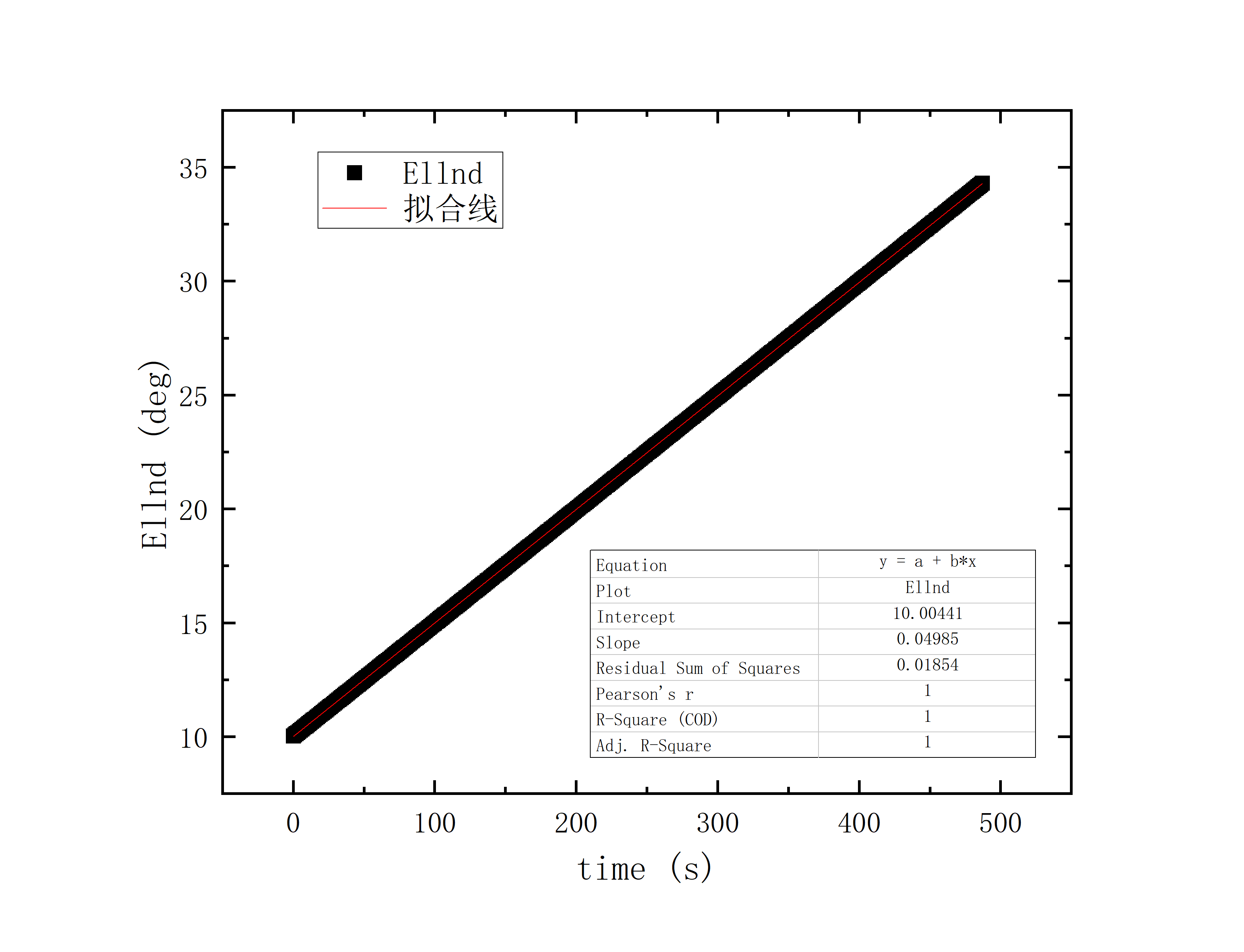
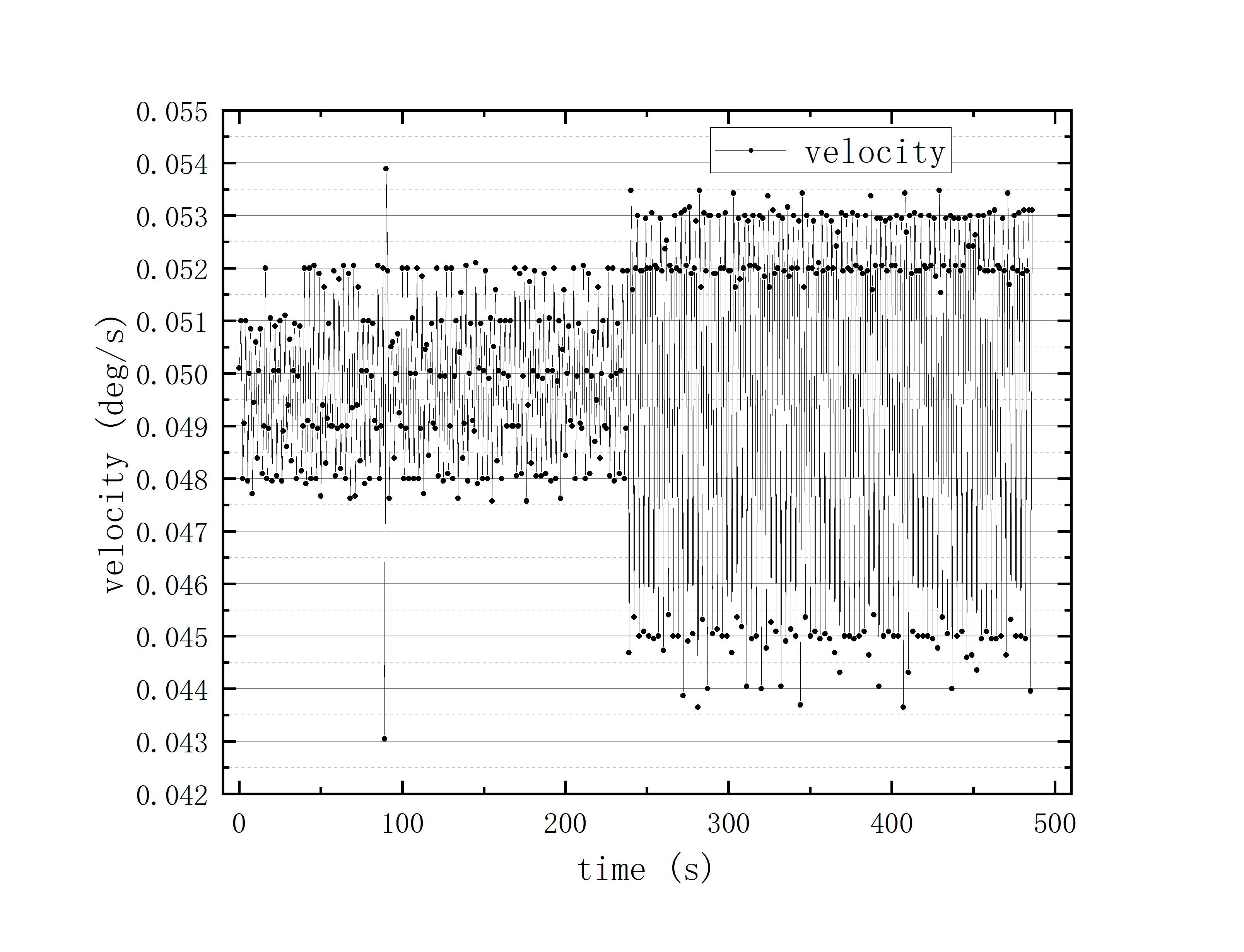
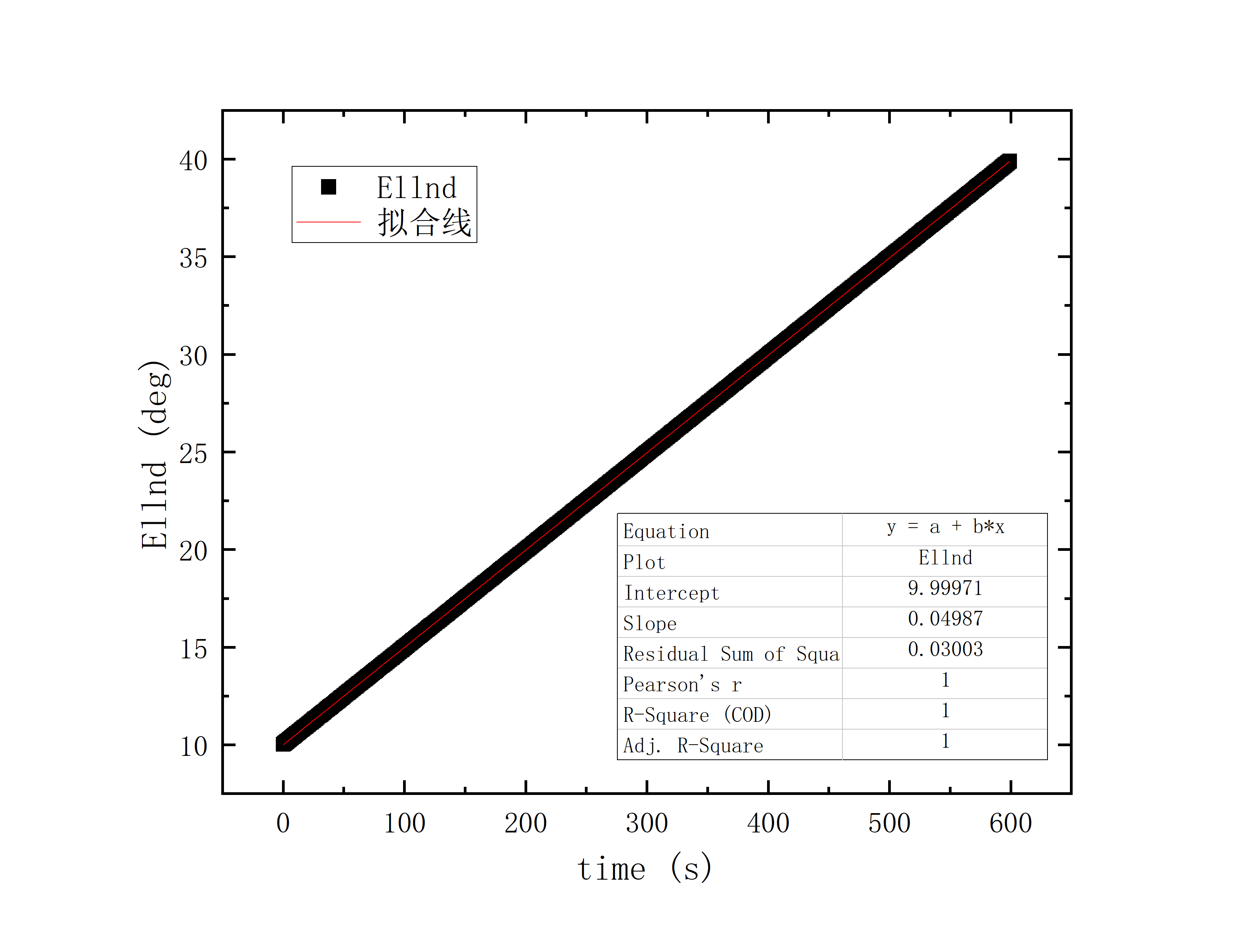
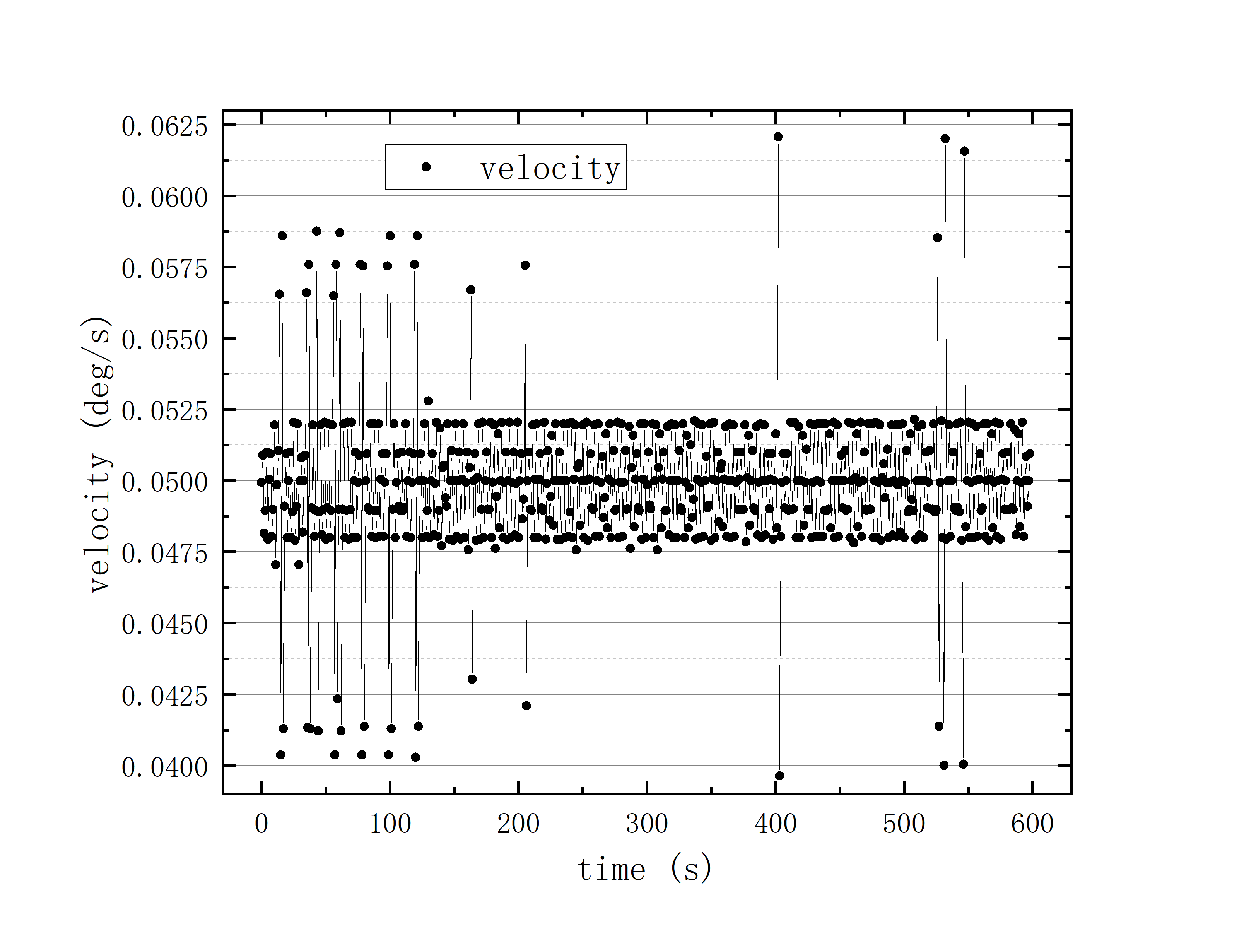
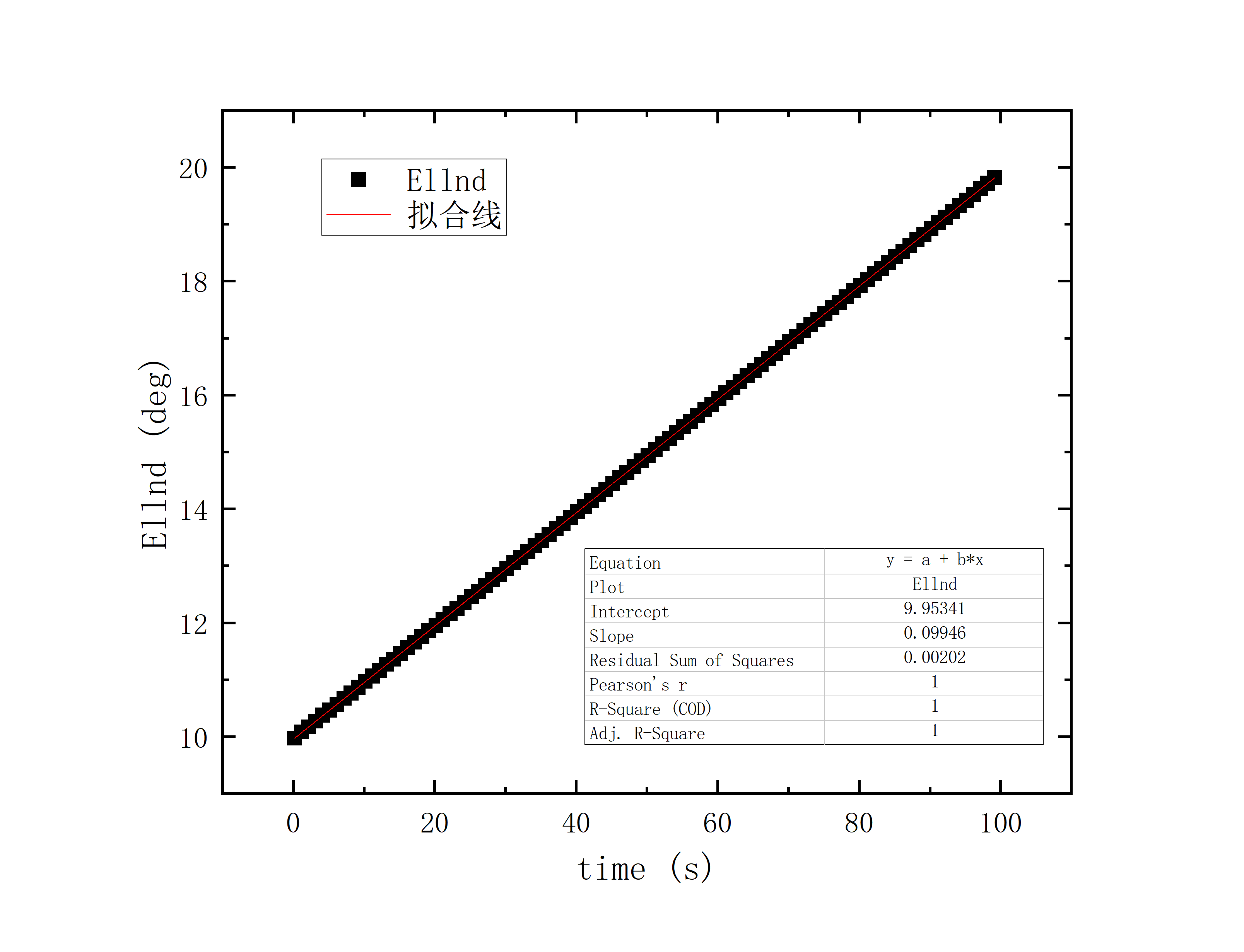
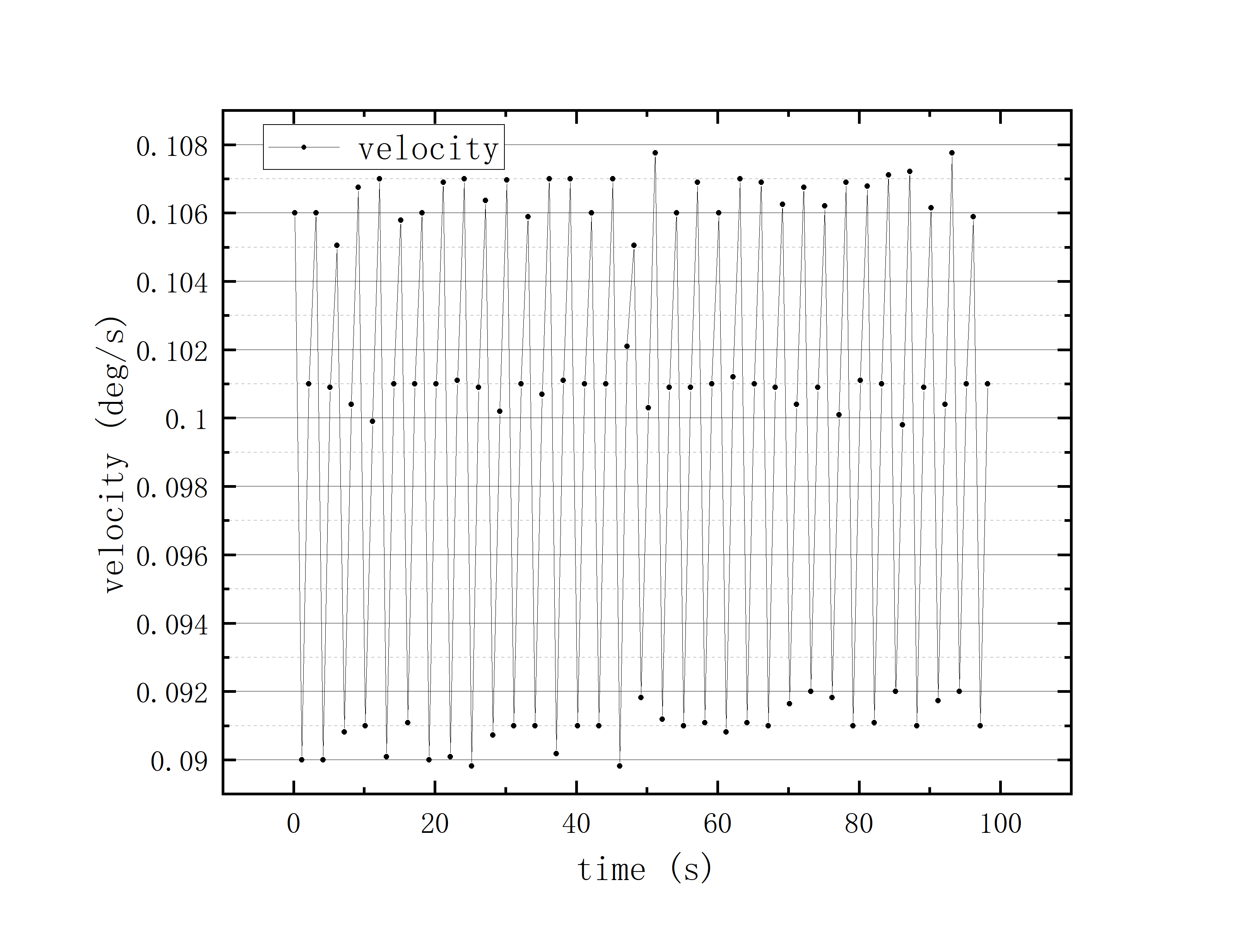
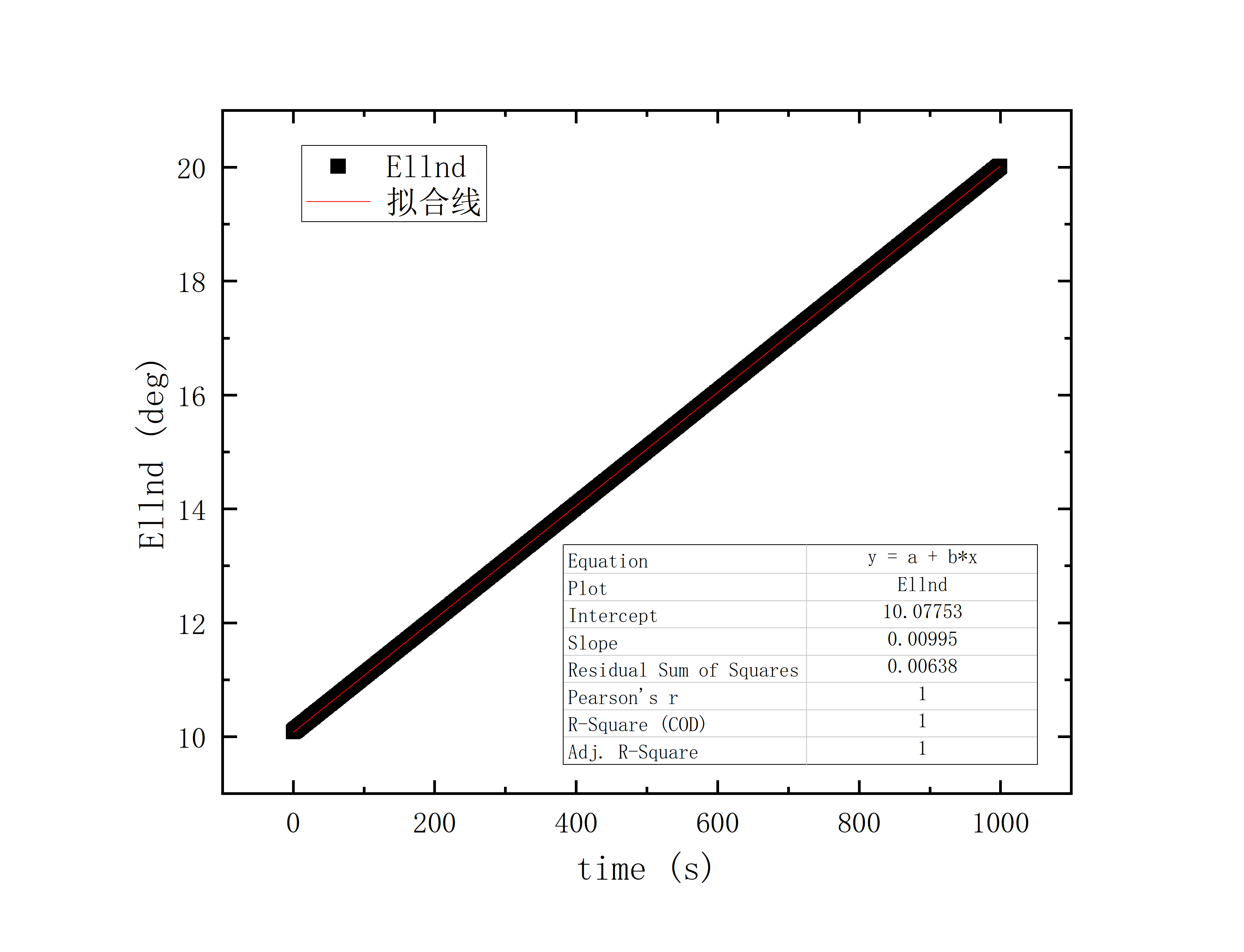
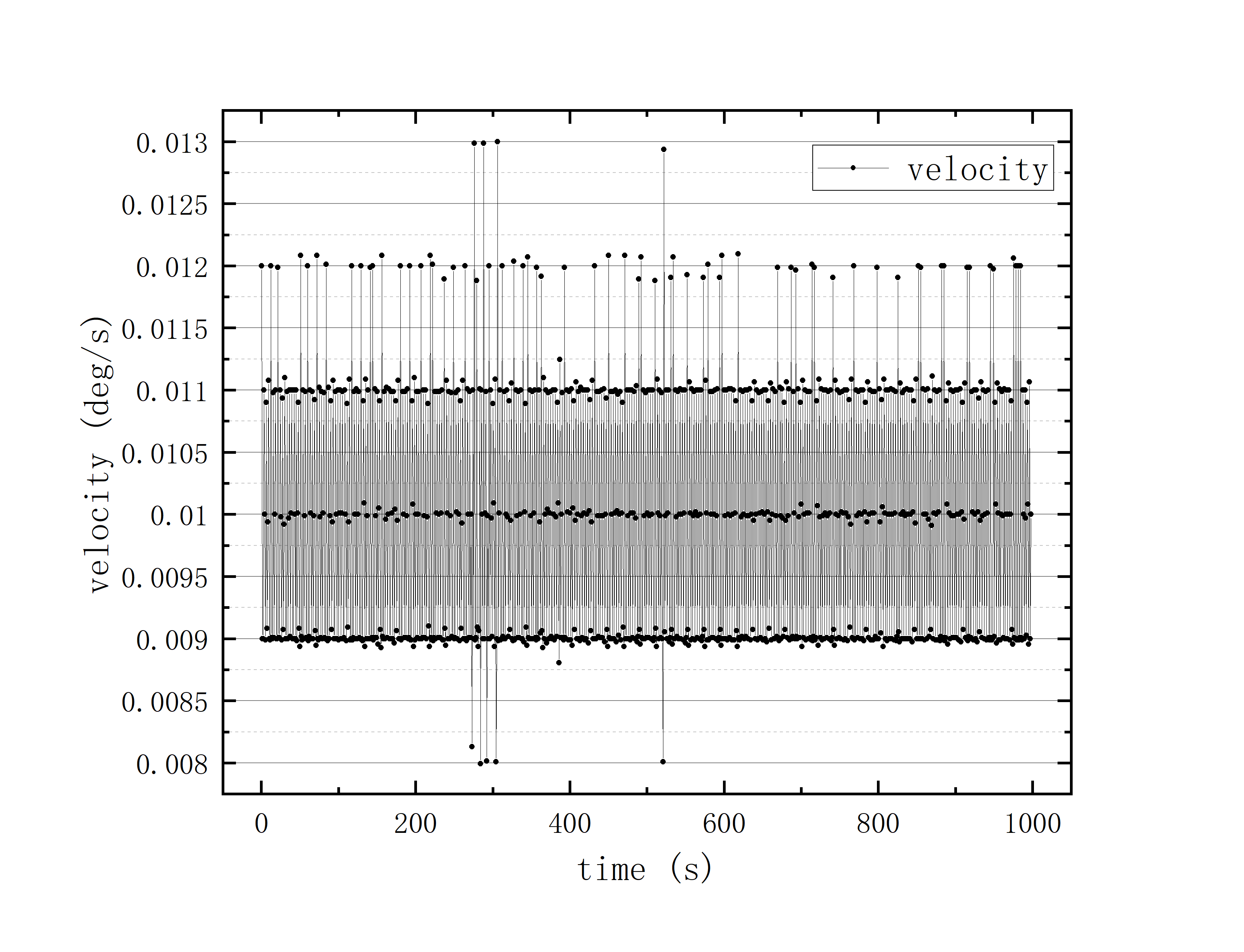
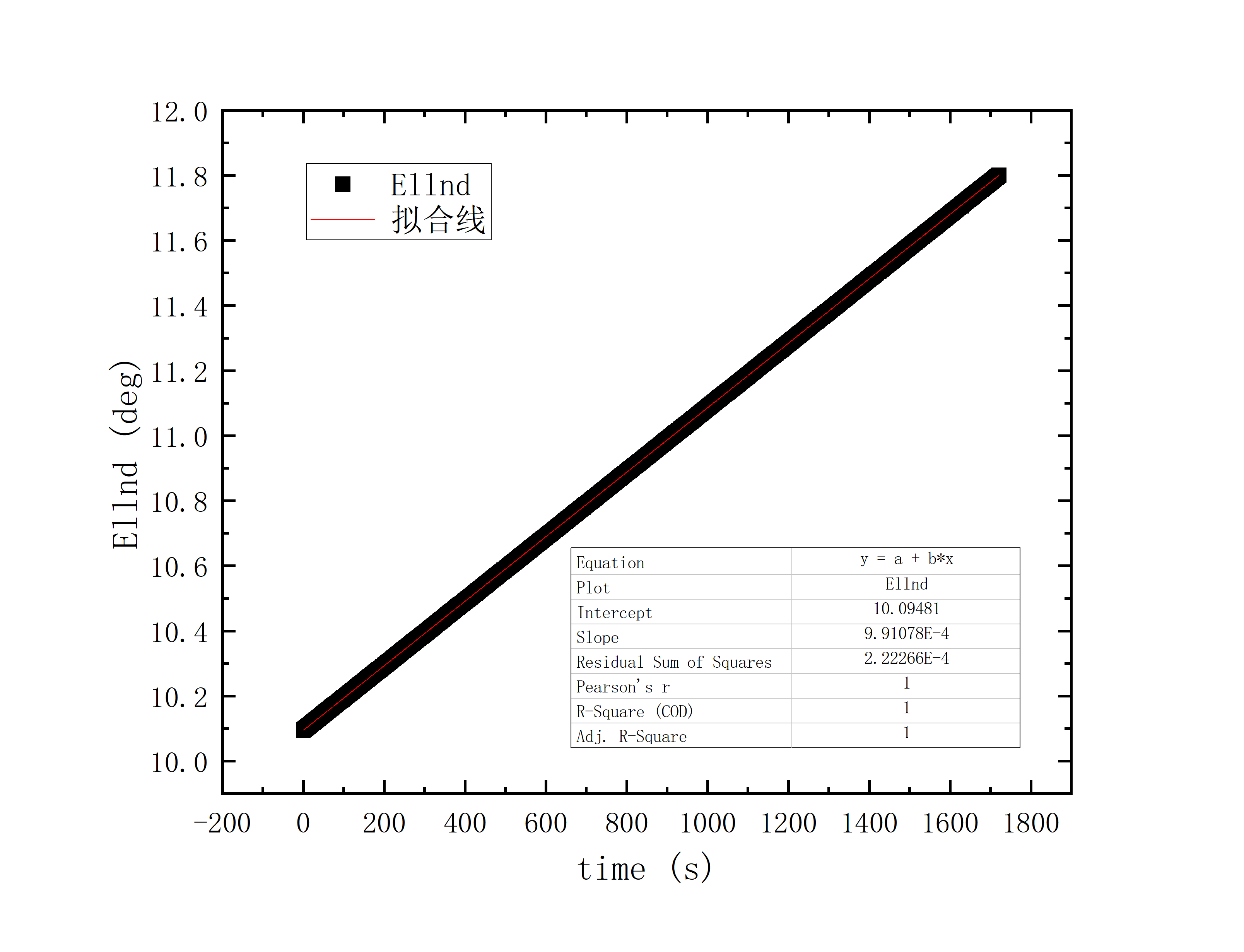
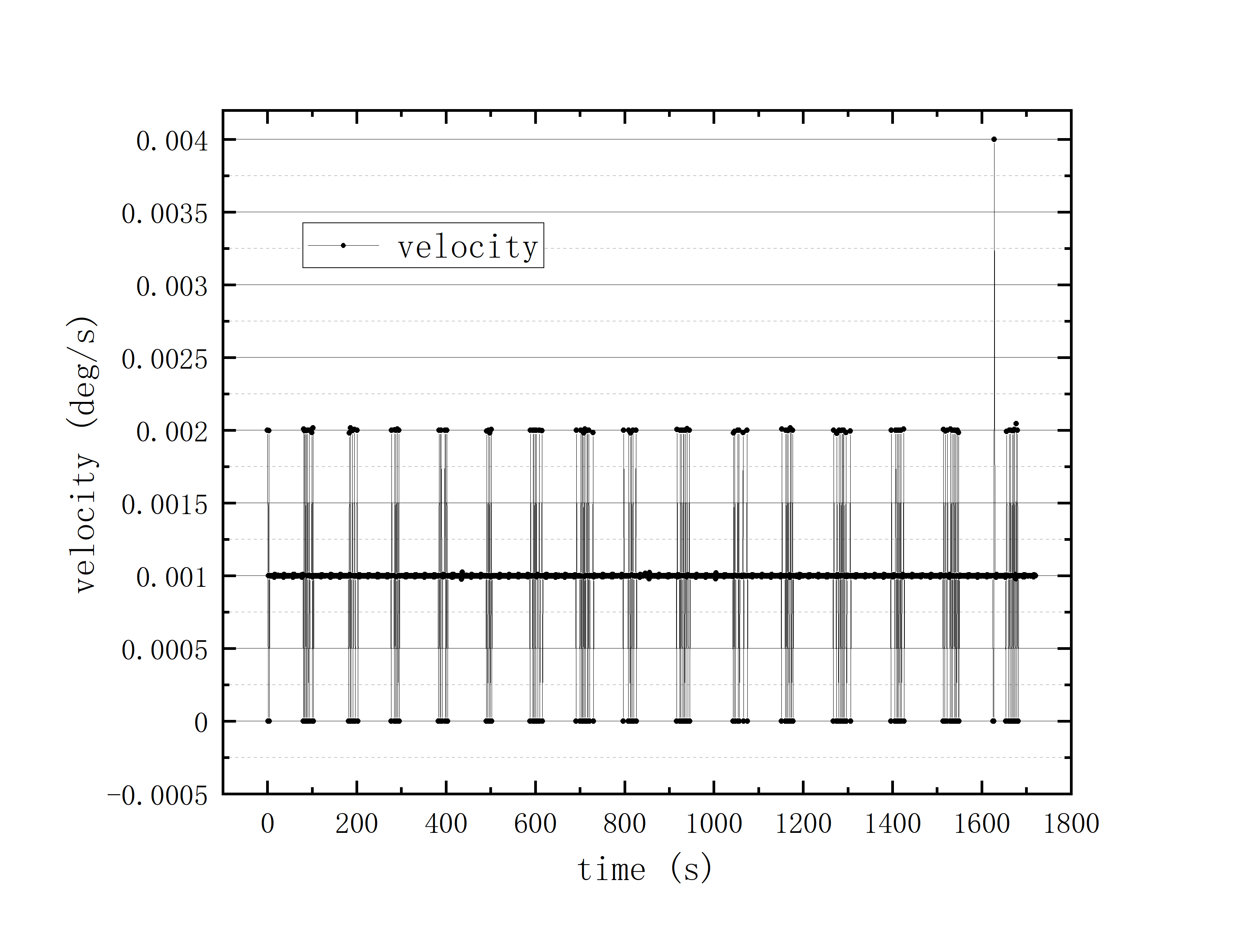
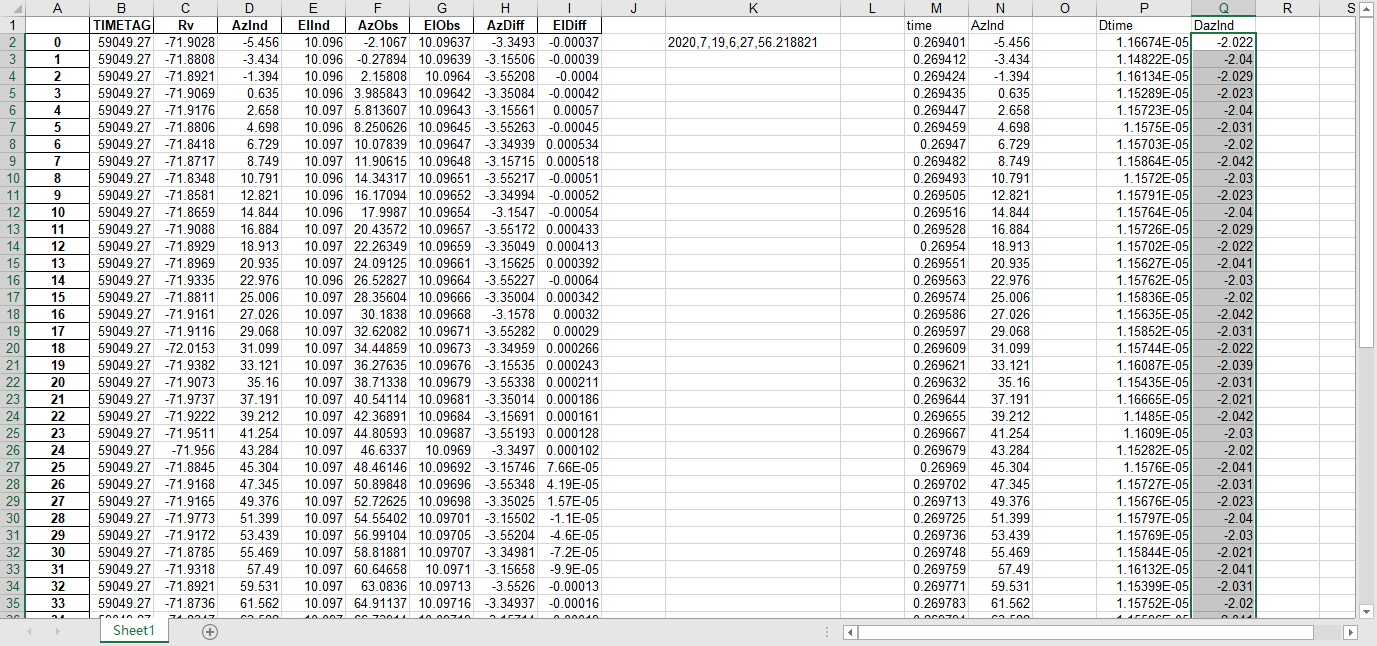
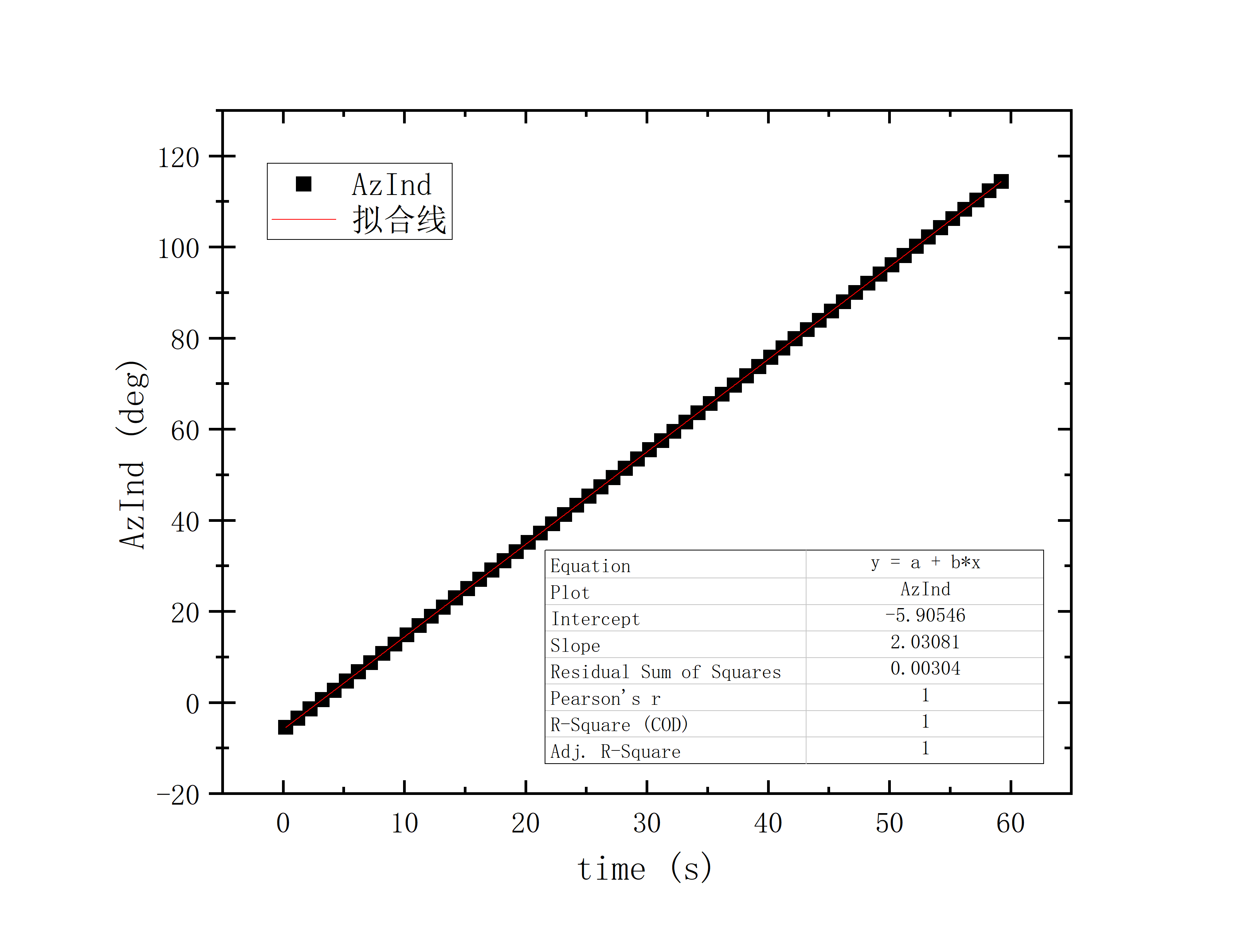
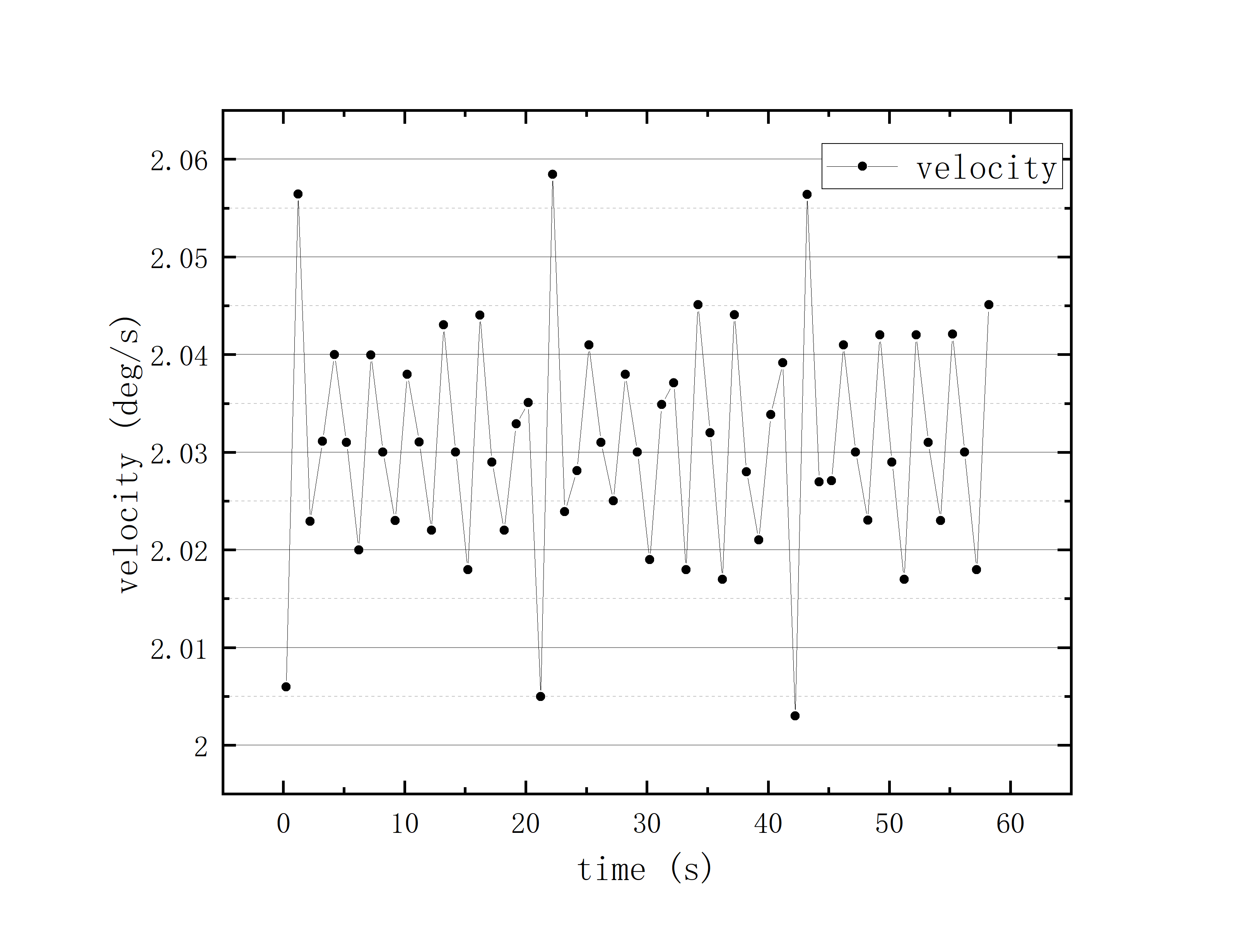
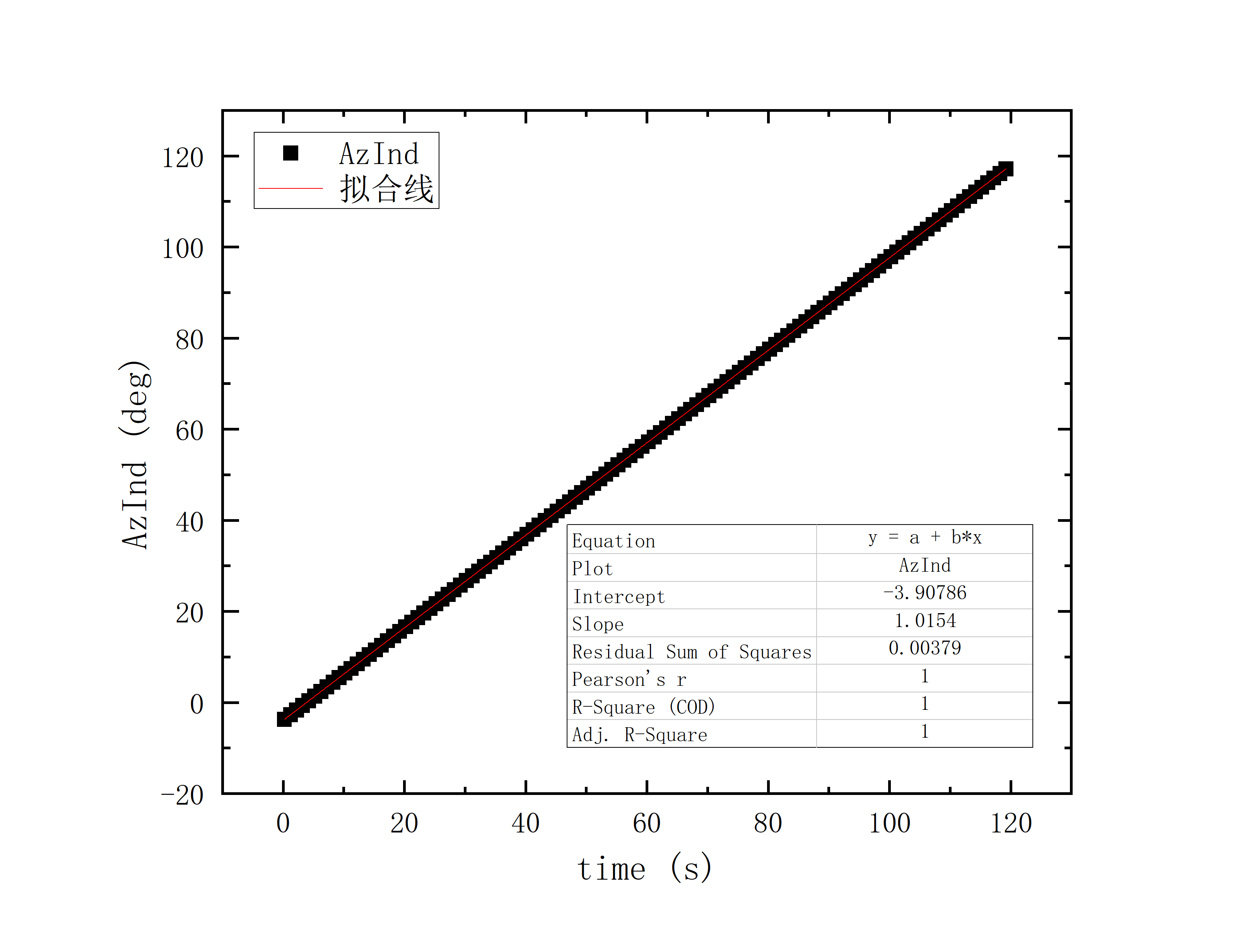
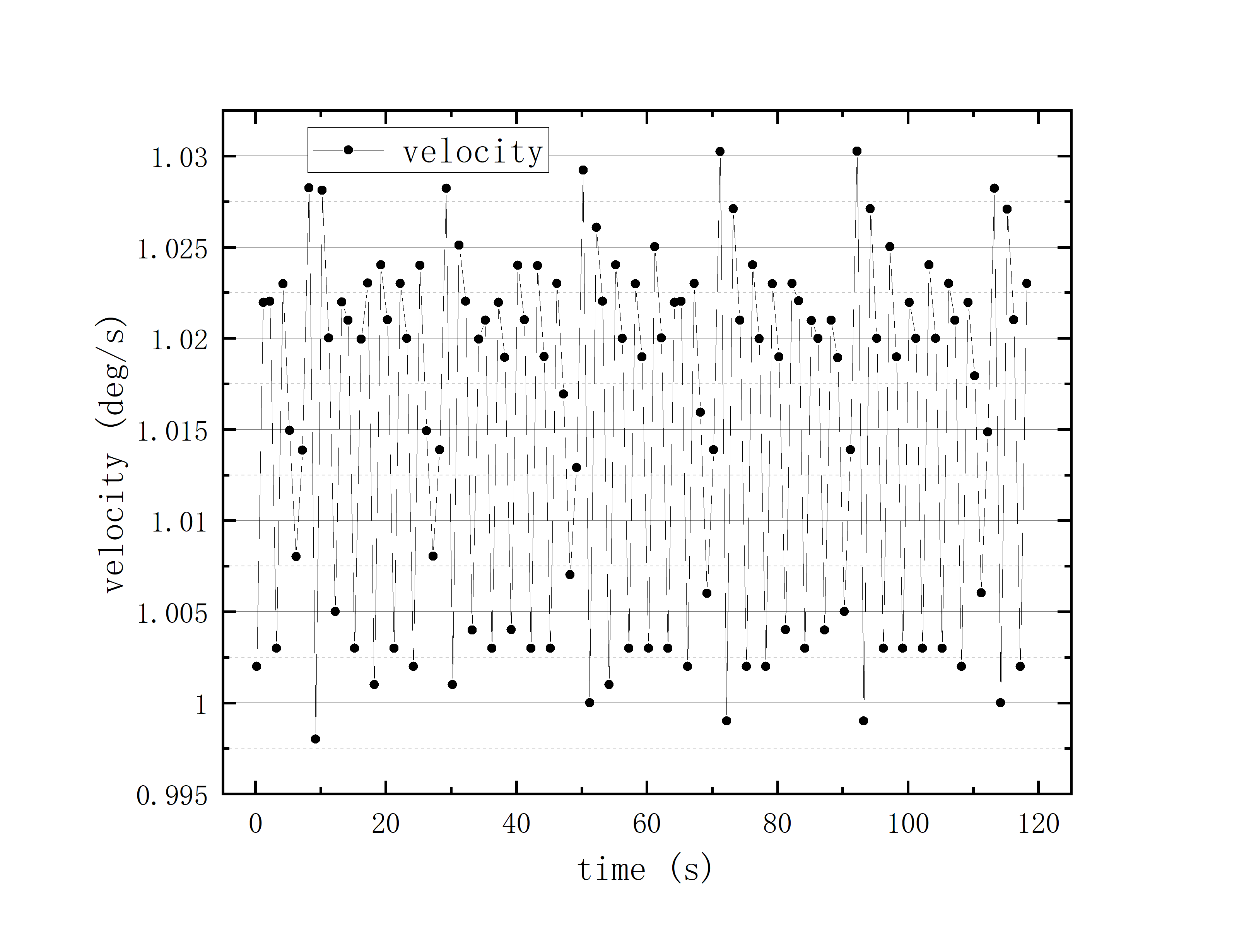
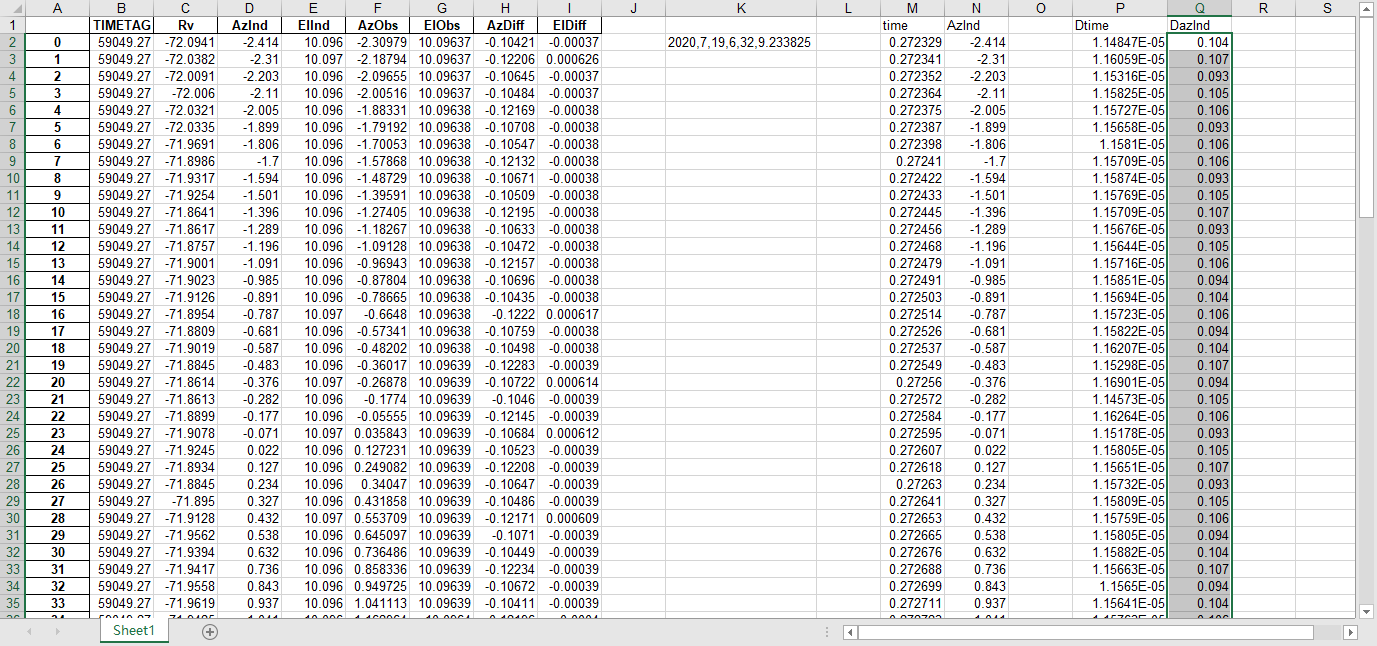
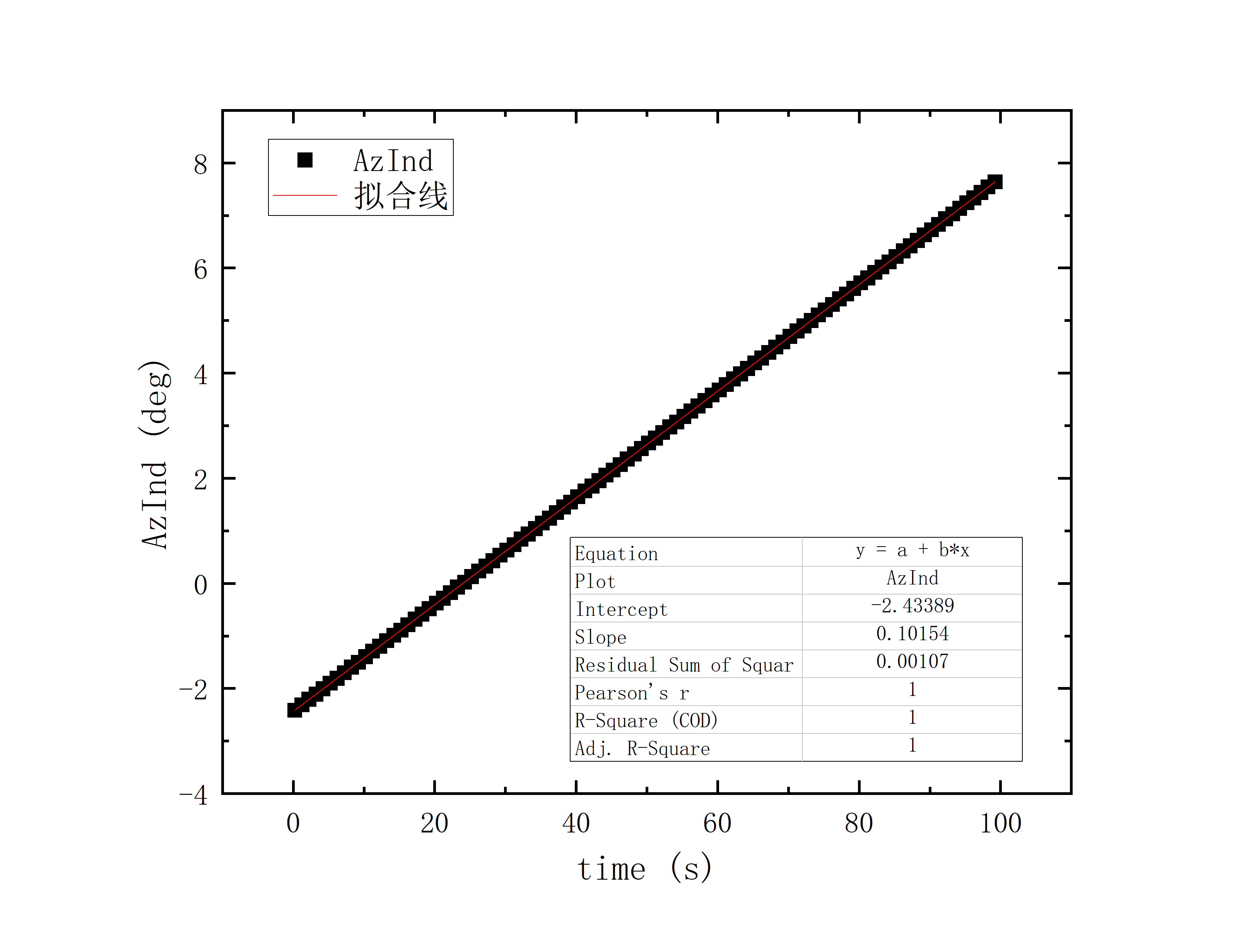
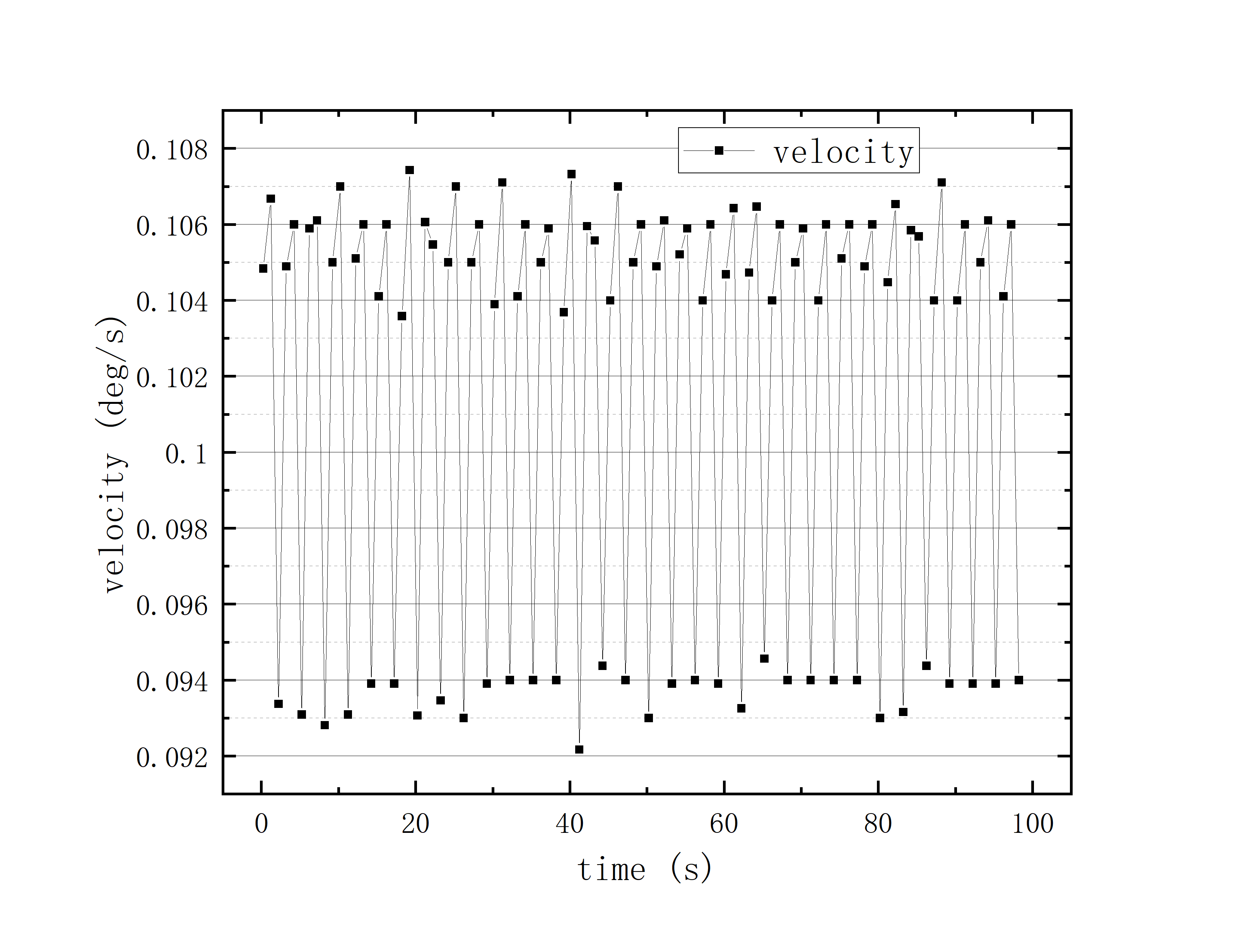
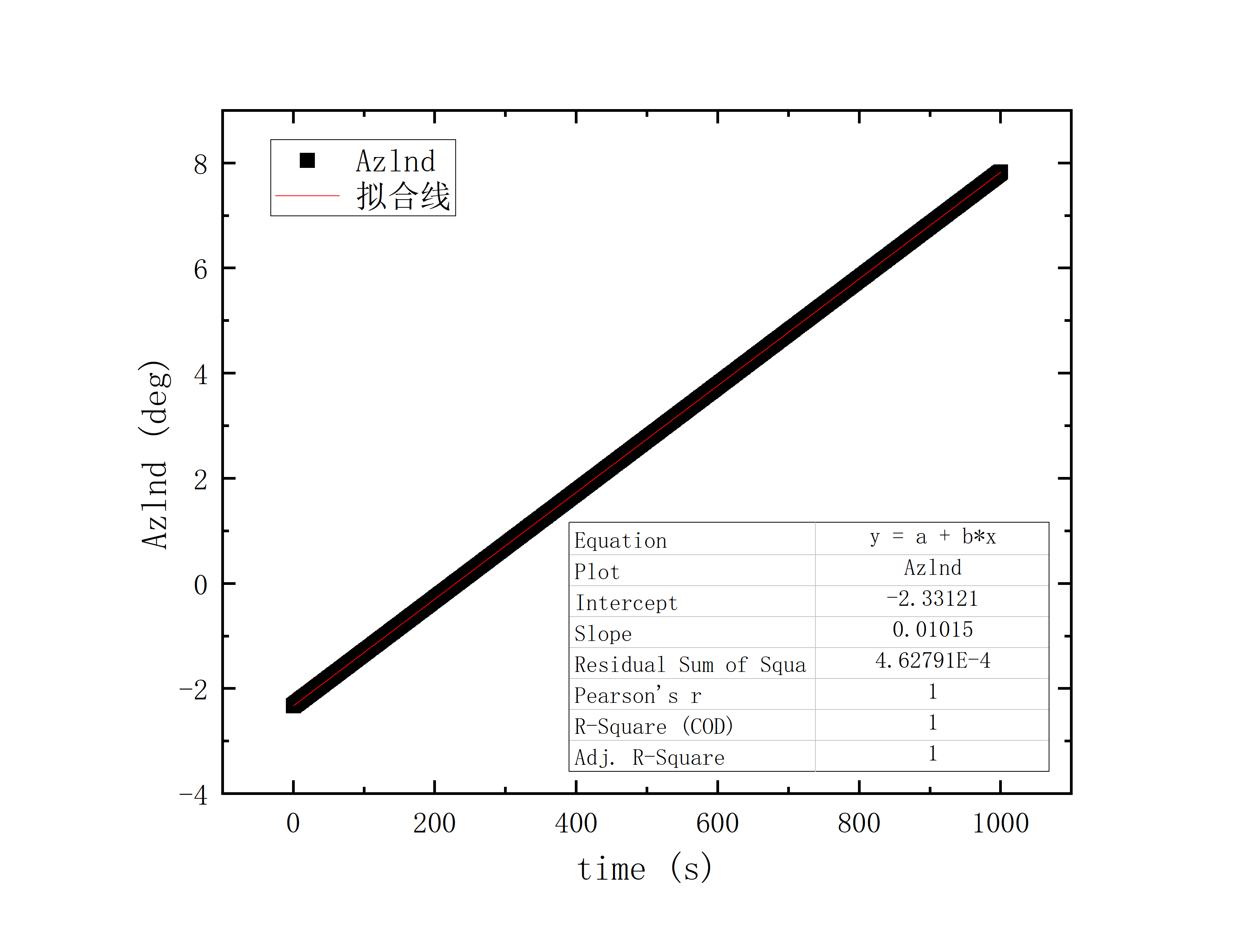
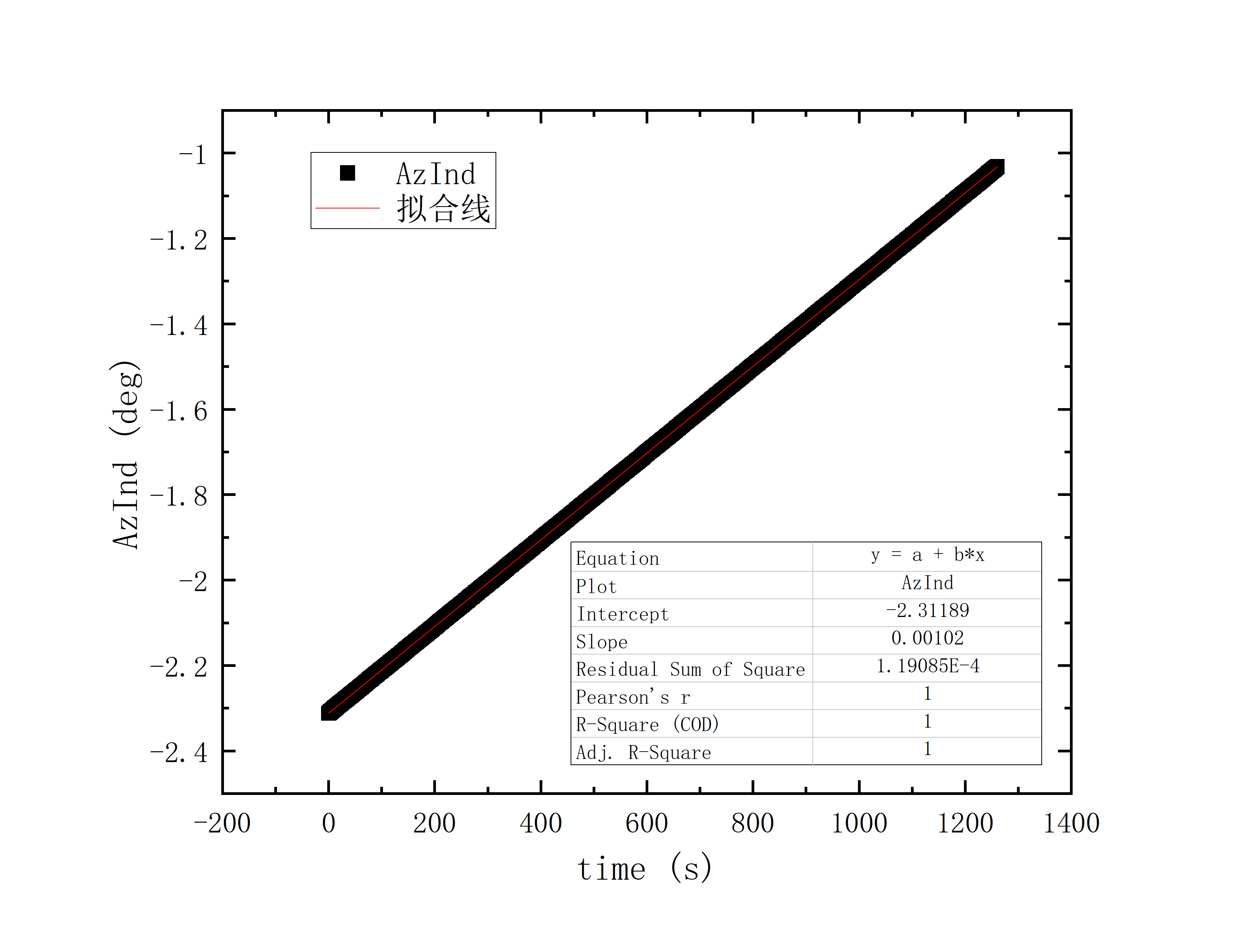
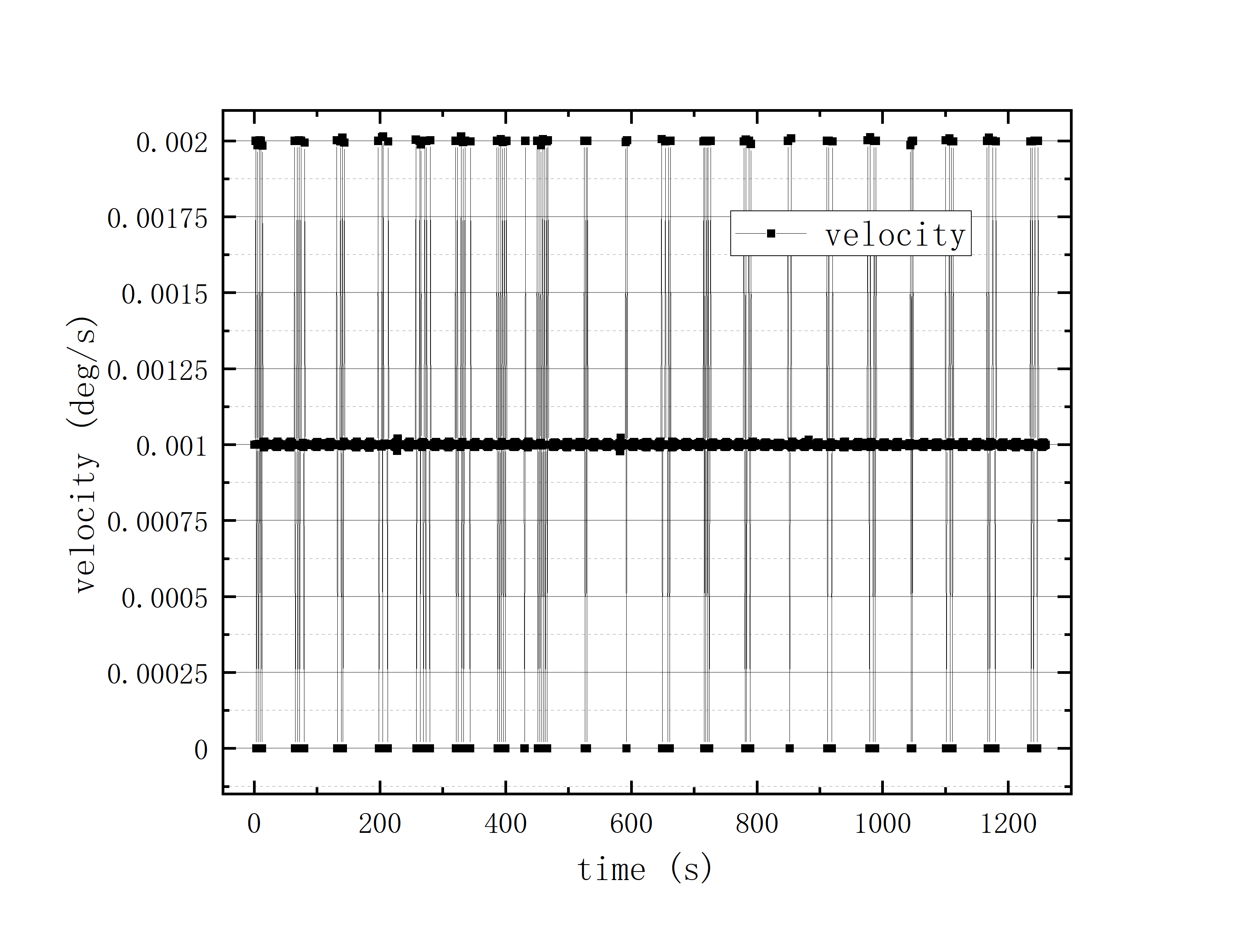
文件提取到excel后使用originlab软件进行画图和拟合操作，画出时间和方位/俯仰的平面图，后进行拟合。图例中给出拟合参数，对方位/俯仰做差与邻近时间做差进行相除，给出加速度图例图中使用Acc（acceleration）。其中要说明time（时间）是简化儒略日的数值给小数点前的取零，因为简化儒略日也是线性的对作图并不影响，所以没有进行转化。

基本统计概念

在展示数据之前提供的拟合参数做简略的解释：

残差（residual）

残差在数理统计中是指实际观察值与估计值（拟合值）之间的差。“残差”蕴含了有关模型基本假设的重要信息。如果回归模型正确的话， 我们可以将残差看作误差的观测值。

总离差平方和/总平方和（Total Sum of Squares，TSS）

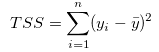
回归平方和/解释平方和 或者下文中的SSreg（Explained Sum of Squars，ESS）

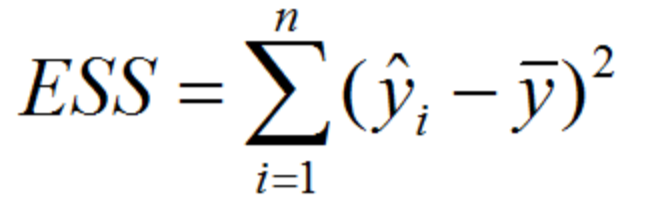
其中需要解释TSS=RSS+ESS，图中的sst、sse、ssr就是TSS、ESS、RSS。

拟合图片中给出的参数解释

1. 残差平方和（Residual sum of squares，RSS）
   为了明确变量和随机误差各自产生的效应是多少，统计学上把数据点与它在回归线（拟合线）上的位置差异称为残差，把每个残差平方后加起来称为残差平方和，表示了随机误差的效应。一组数据的残差平方和越小，其拟合度越好！

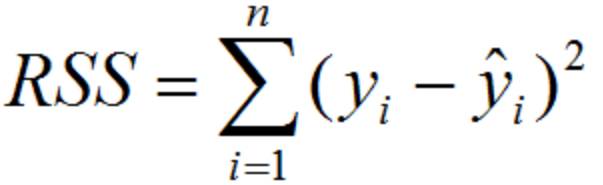
1. 皮尔森相关系数（Pearson’s R）
   皮尔森相关系数可以衡量配对数据之间的线性关系。Pearson’s R的极限值在-1和1之间。在线性回归钟，Pearson’s R的正值表明变量x和变量之间存在线性正相关，而Pearson’s R的负值表示变量x和变量之间存在线性负相关。0则表示数据之间没有线性相关关系。而且，该值越接近-1或者1，线性相关关系越强。

2. R-Square（Coefficient of determination，COD）
   也叫Coefficient of determination，是一种用于量化线性回归的统计量度。它是拟合的回归线所解释的响应量变化的百分比，例如R-Square表明该模型解释了响应变量中大约超过89％的变化。因此，R-Square始终在0到1之间。如果R平方为0，则表明拟合线不能解释响应数据均值附近的变化。如果R平方为1，则表示拟合线解释了响应数据均值附近的所有变化。通常，R-Square越大，拟合线越适合您的数据。再结合下面的公式可以看出，当使用良好拟合模型时，R-Square应在0 到1之间变化。接近1的值表示该拟合为良好的模型。

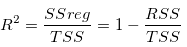
1. Adj.R-Square
   在R-Square已经讲到：R-Square可以用于量化模型对数据的拟合程度，当添加新的预测变量时，R-Square将始终增加。一个具有更多预测变量的模型具有更好的拟合度是一个误解。 Adj.R-Square 是对R-Square的一个修改版本，已针对拟合中的预测变量数进行调整。因此，它可以用于与具有不同数量预测变量的拟合线进行比较。如果预测变量大于1，则Adj.R-Square 始终小于R-Square。再结合下面的公式可以看出，当使用良好拟合模型时，Adj.R-Square应在0 到1之间变化。接近1的值表示该拟合为良好的模型。

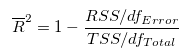
2020_07_19_04_32_34

2020_07_19_04_45_12

2020_07_19_04_51_08

2020_07_19_05_02_52

2020_07_19_05_17_28

2020_07_19_05_35_17

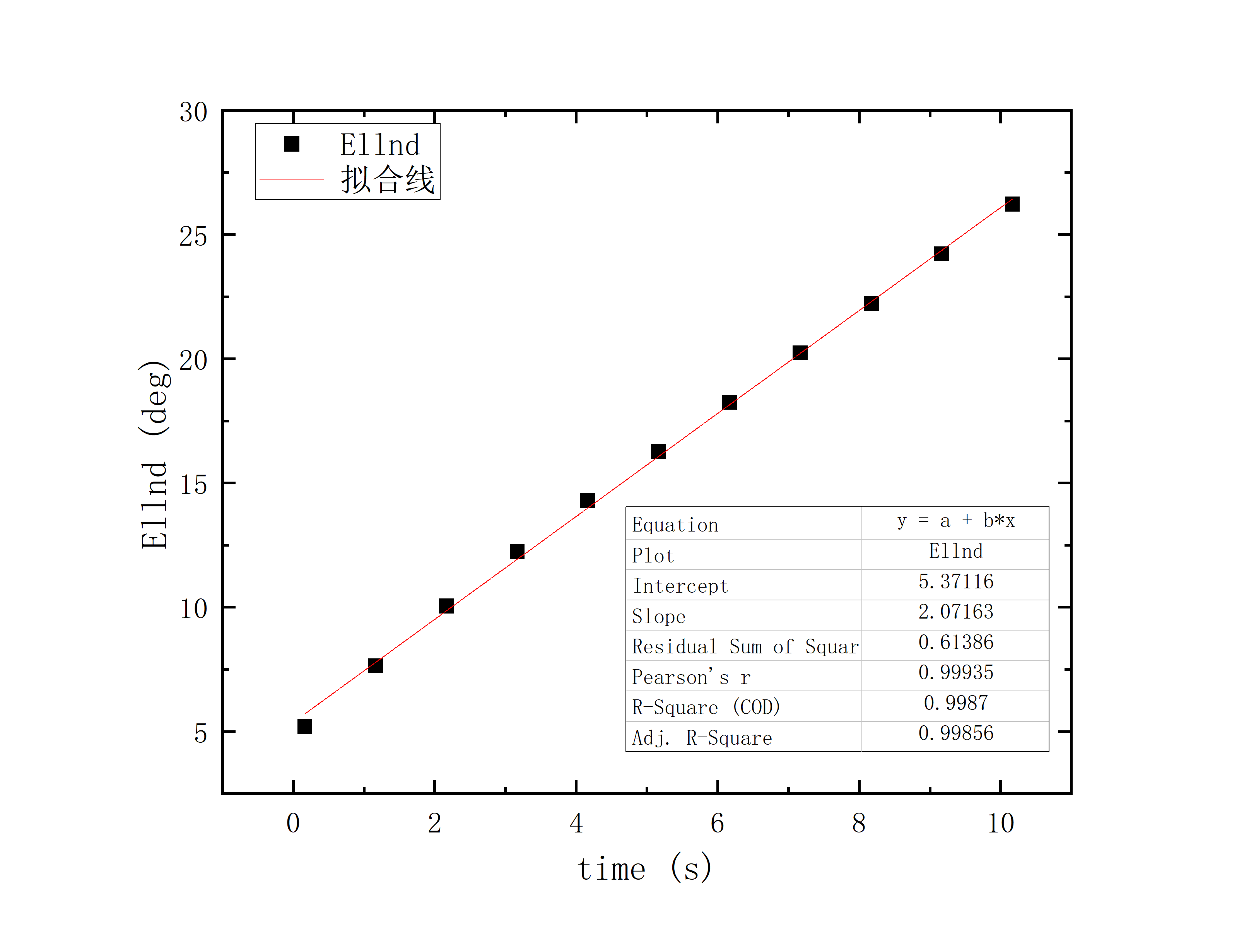
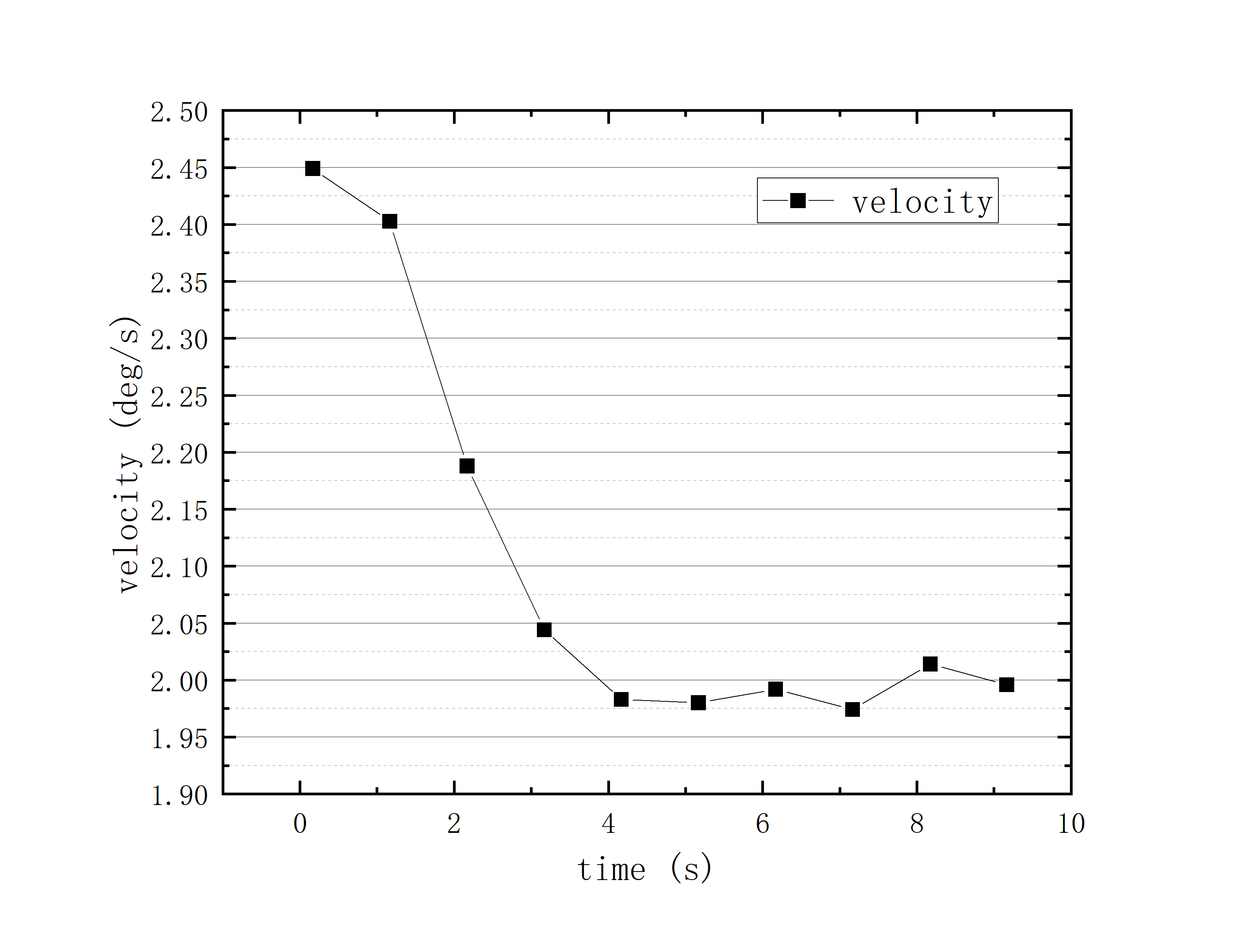
2020_07_19_05_37_05

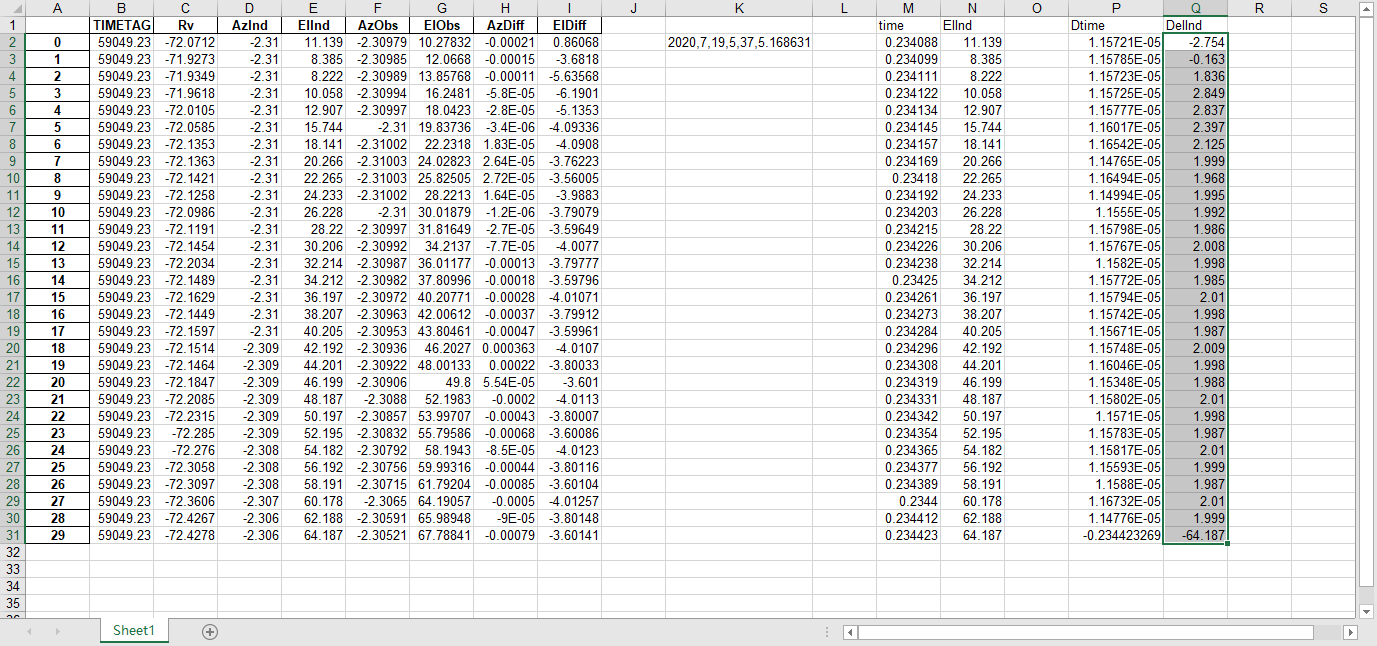
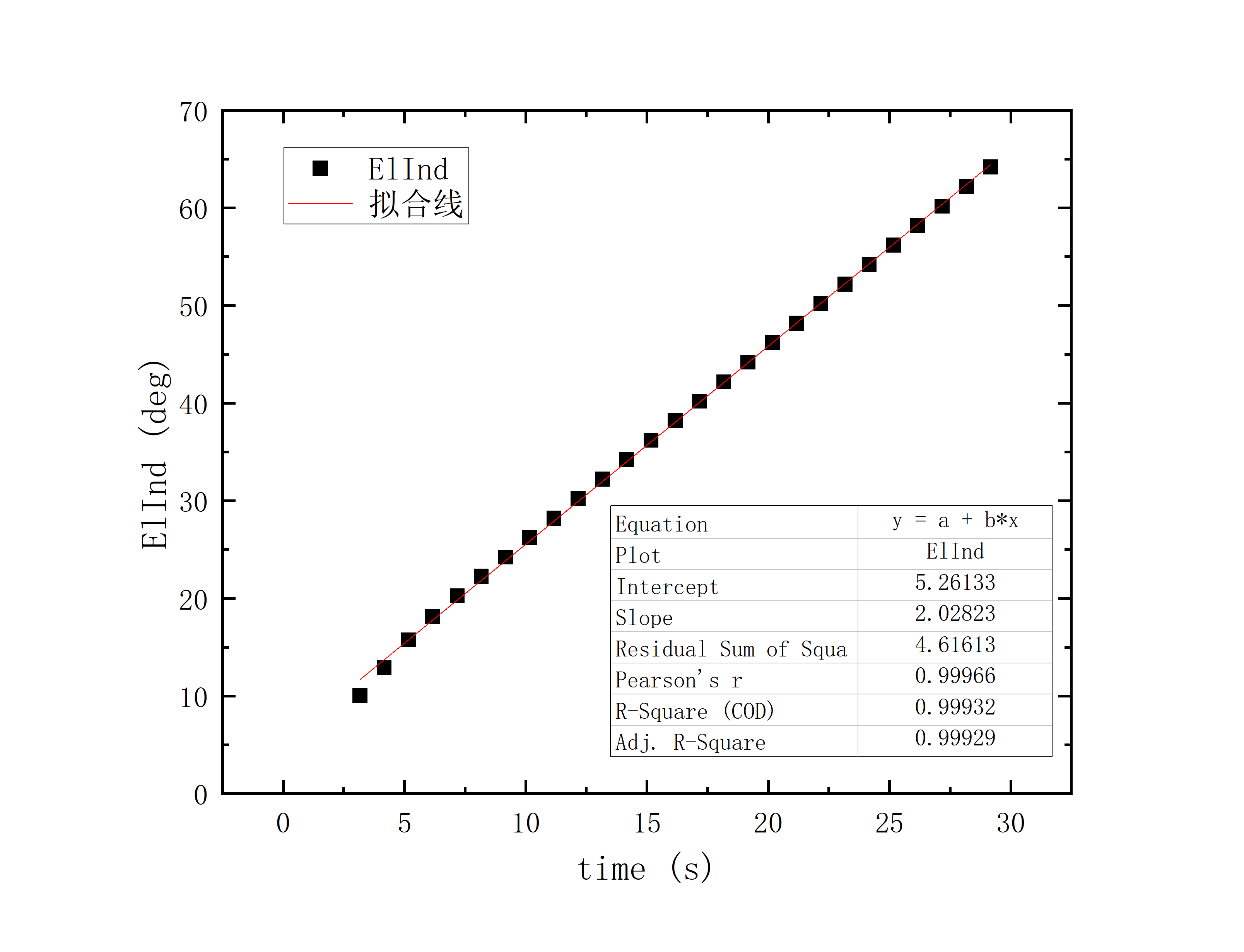
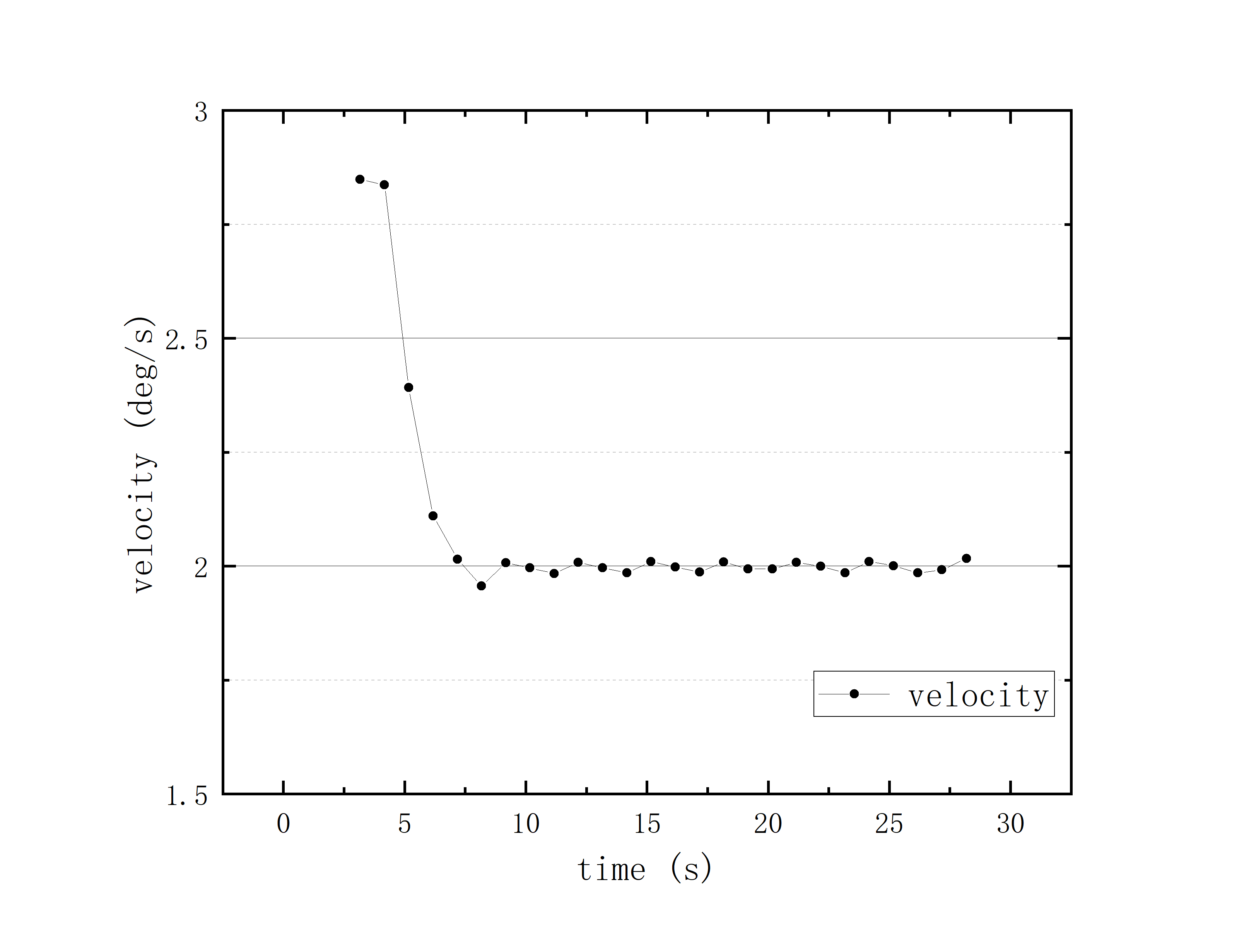
2020_07_19_05_38_08

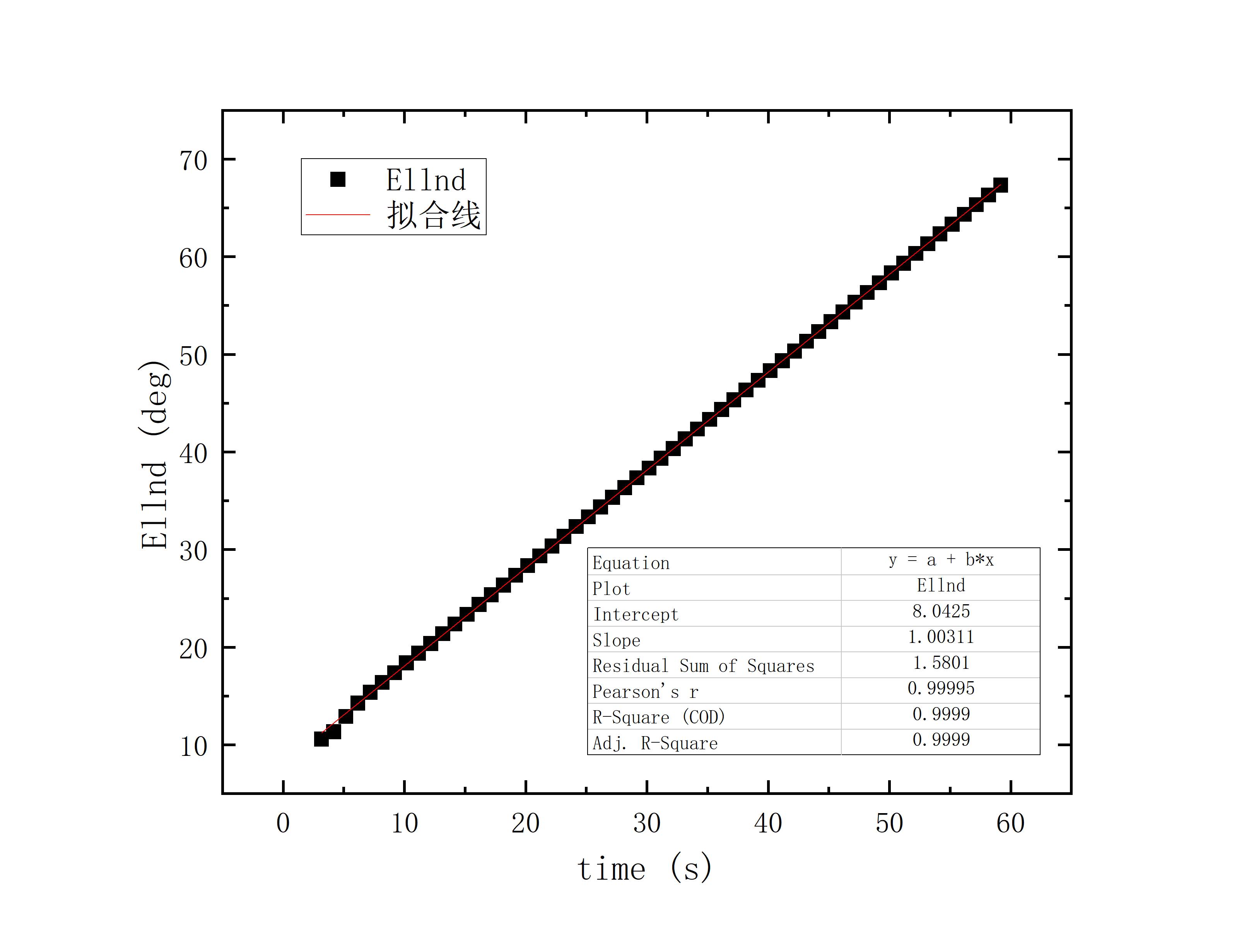
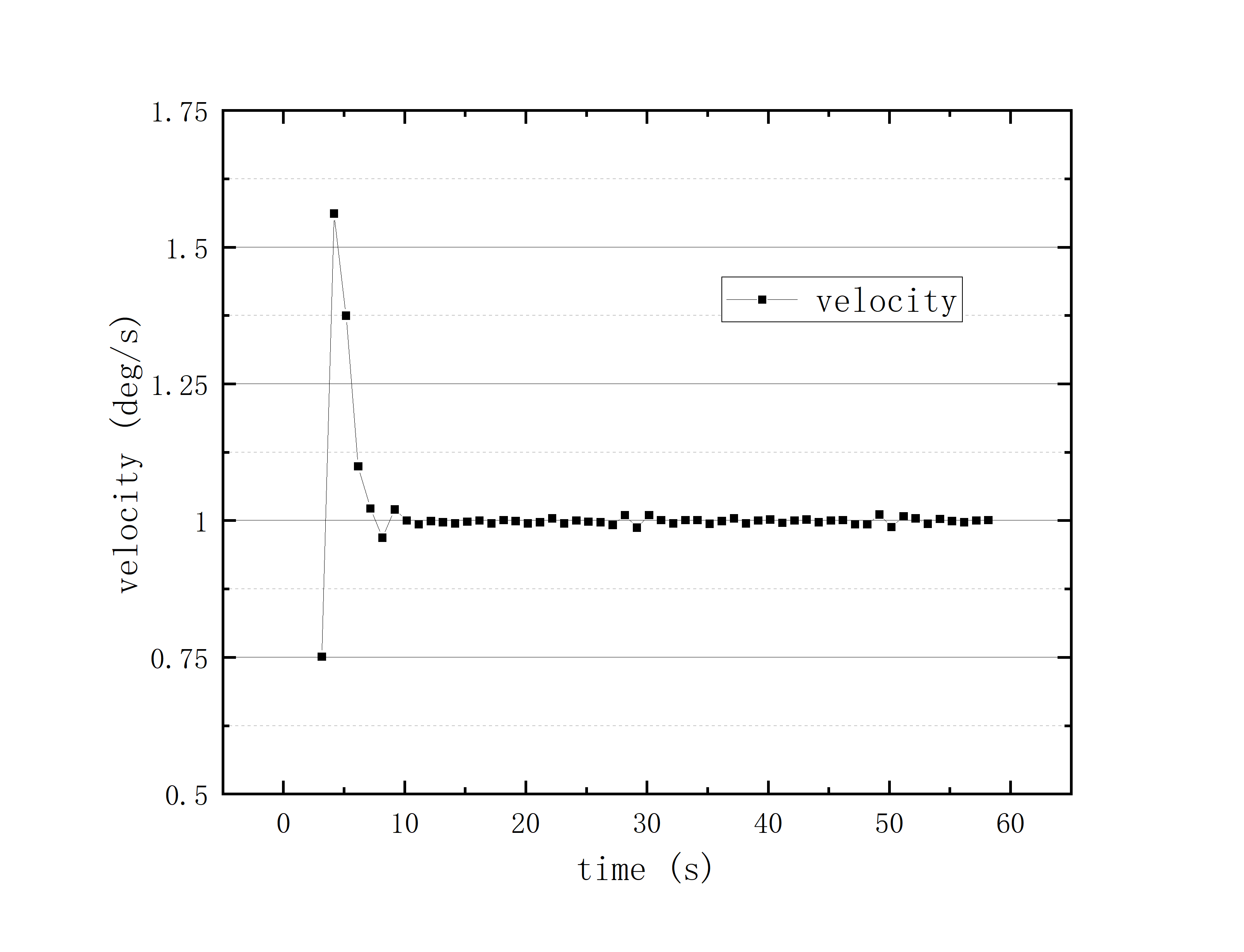
2020_07_19_05_39_38

2020_07_19_05_41_38

2020_07_19_05_58_38

2020_07_19_06_27_56

2020_07_19_06_29_34

2020_07_19_06_32_09

2020_07_19_06_34_09

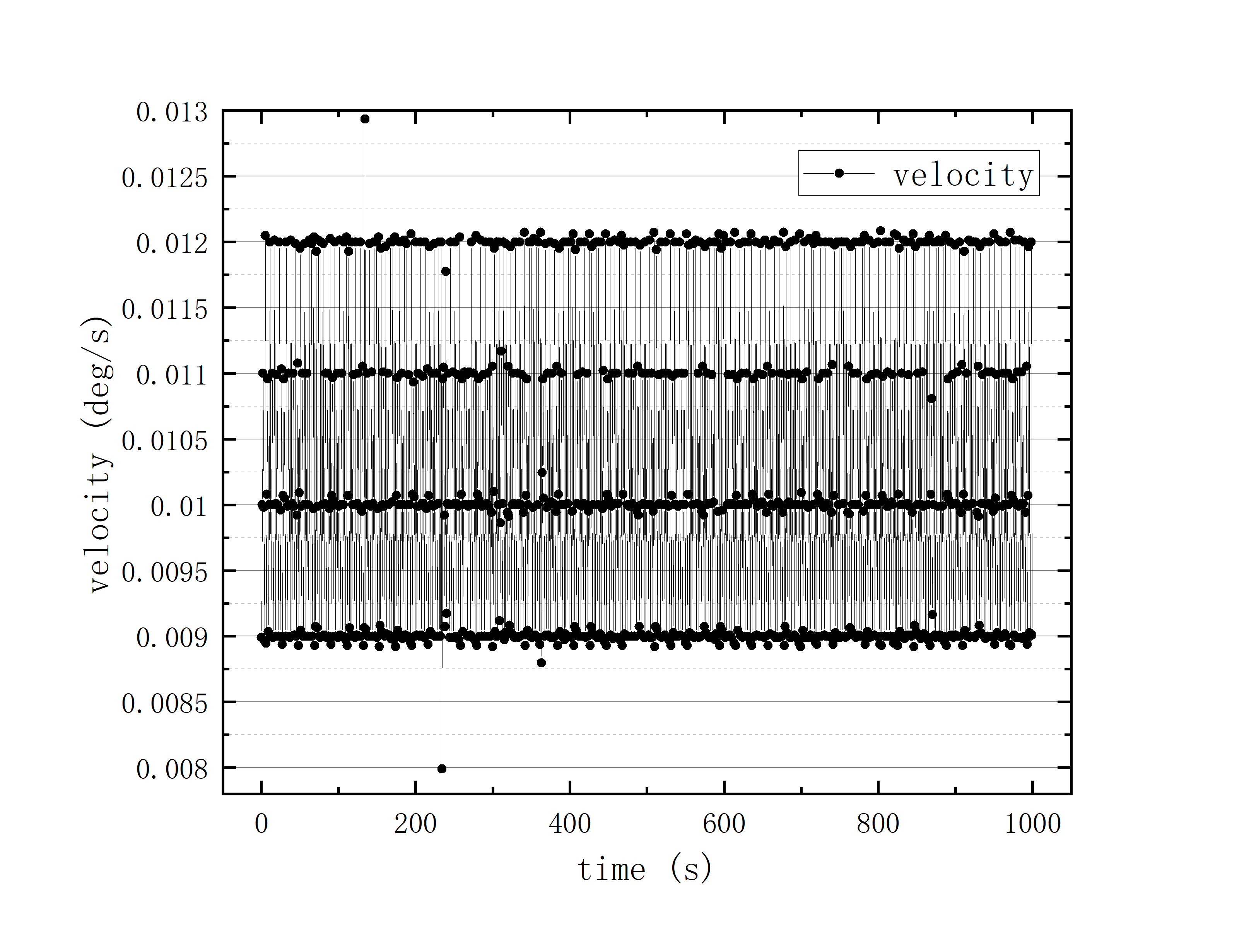
2020_07_19_06_51_09

总结

可以看到几乎所有的拟合参数都显示一个非常好的线性的拟合，且速度的波动都集中在非常小的范围内。除了在天线启动、停止时造成的速度变化较大（例如：2020_07_19_05_37_05、2020_07_19_05_38_08），和数据点较少时看上去的“速度波动”（例如：2020_07_19_05_35_17）外，多数速度波动都在较小的范围内波动。